Kezdőlap


Feladat:	Gy.2106	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1983/november, 141 - 142. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Síkgeometriai számítások trigonometria nélkül, Gyakorlat, Szabályos sokszögek geometriája
Hivatkozás(ok):	Feladatok: 1983/február: Gy.2106

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A háromszög szimmetriatengelyei az $O$ középpontot a csúcsokkal összekötő egyenesek. Tekintsük ezeknek az $O A$ , $O F$ , $O B$ félegyeneseit, ahol $F$ az $A B$ oldal felezőpontja. Az érintő köröknek ezekre illeszkedő középpontjait jelölje rendre $O_{1}$ , $O_{2}$ és $O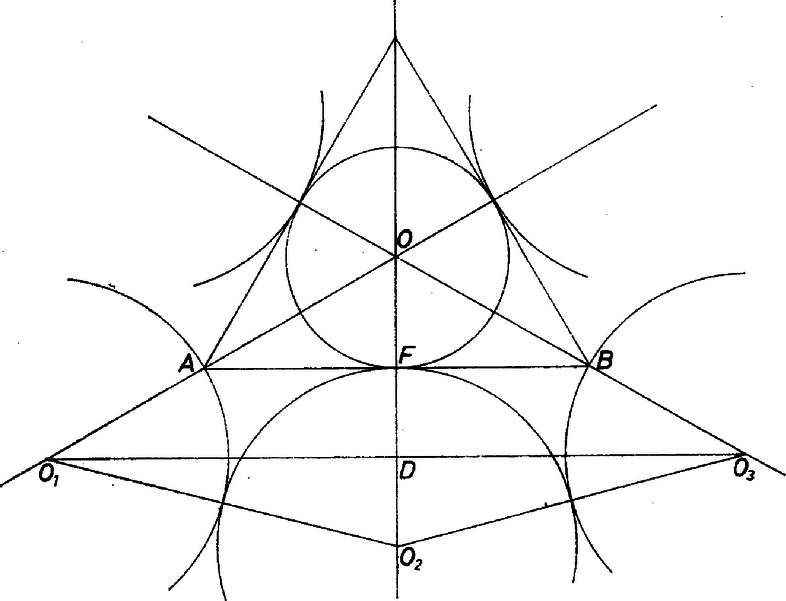_{3}$ (1. ábra).

1. ábra

Mivel a köröknek a háromszöggel csak egy közös pontjuk van, az érintési pontok rendre az

A

F

B

pontok. Így

A O_{1} = F O_{2} = B O_{3} = R

az érintő körök sugara. Mivel e körök egymást is érintik,

O_{1} O_{2} = O_{2} O_{3} = 2 R

, továbbá

O F = r

O A = O B = 2 r

és

F B = r \sqrt[]{3}

ahol

r

a háromszögbe írt kör sugara.
Az

O_{1} O O_{3} O_{2}

négyszög deltoid, ezért átlói merőlegesek egymásra. Legyen metszéspontjuk

D

. Az

O F B

és

O D O_{3}

háromszögek hasonlóságából

\begin{matrix} D O_{3} = \frac{O O_{3} \cdot F B}{O B} = \sqrt[]{3} \frac{2 r + R}{2}, és D O = \frac{O O_{3} \cdot F O}{O B} = \frac{2 r + R}{2} . \end{matrix}

Ez utóbbiból

D O_{2} = O O_{2} - D O = (r + R) - D O = R / 2

. Írjuk fel a

D O_{2} O_{3}

D

-ben derékszögű háromszög oldalaira a Pitagorasz‐tételt:

\begin{matrix} {(\frac{R}{2})}^{2} + {(\sqrt[]{3} \frac{2 r + R}{2})}^{2} = {(2 R)}^{2} . \end{matrix}

Rendezve

r

-re másodfokú egyenletet kapunk:

r^{2} + R r - R^{2} = 0

, ahonnan

\begin{matrix} r = \frac{R (\sqrt[]{5} - 1)}{2}, \end{matrix}

mivel

R

és

r

egyaránt pozitív.

Most nézzük meg, milyen összefüggés áll fenn az

O

középpontú,

R

sugarú körbe írt szabályos tízszög

a

oldala és

R

között (2. ábra).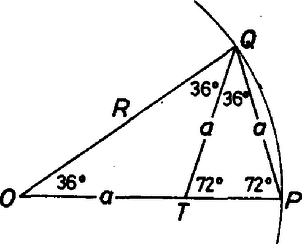

2. ábra

A tízszög

P Q

oldalához tartozó

P O Q

középponti szög

36^{\circ}

-os. A

P O Q

egyenlő szárú háromszögben húzzuk meg az

O Q P

72^{\circ}

-os szög belső szögfelezőjét, messe ez az

O P

oldalt

T

-ben. Ezzel két egyenlő szárú háromszöget,

P Q T

-t és

Q T O

-t kaptunk, tehát

P Q = Q T = T 0 = a

. A

P Q T

és

P O Q

háromszögek hasonlók, hiszen szögeik megegyeznek. Megfelelő oldalaik aránya

\begin{matrix} \frac{a}{R} = \frac{P Q}{O P} = \frac{P T}{P Q} = \frac{R - a}{a} . \end{matrix}

Rendezés után

a^{2} + a R - R^{2} = 0

, amiből

a = \frac{R (\sqrt[]{5} - 1)}{2}

. Ugyanazt az értéket kaptuk, mint előbb. Tehát valóban

a = r

, amit bizonyítani kellett.