Feladat: Gy.2100 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Hraskó András 
Füzet: 1983/november, 139 - 140. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1983/január: Gy.2100

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a hegyesszögű háromszög csúcsait A, B, C-vel, megfelelő szögeit α, β, γ-val úgy, hogy teljesüljön α≦β≦γ<90∘. A magasságok talppontjai legyenek TA, TB, TC, TA az A-val, TB a B-vel és TC a C-vel van szemben.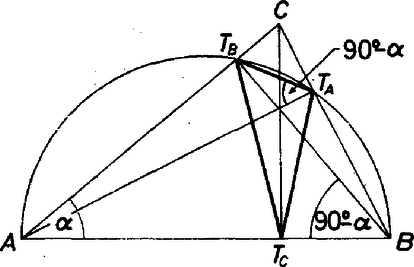

 
 

Az AB oldal Thalész‐körén rajta van TA és TB. Mivel a háromszög hegyesszögű, TA és TB AB-nek ugyanazon partján van, így a kerületi szögek egyenlősége miatt
ABTB∢=ATATB∢=90∘-α.
Hasonlóan a többi oldalon BCTC∢=BTBTC∢=90∘-β és CATA∢=CTCTA∢=90∘-γ.
Ezt felhasználva a talpponti háromszög szögeit kifejezhetjük az α, β, γ szögekkel:
TCTATB∢=180∘-2α,TATBTC∢=180∘-2β,TBTCTA∢=180∘-2γ.
Ezek közül a 180∘-2α legnagyobb a jelölésünk szerint, s emiatt
2α+γ≤α+β+γ=180∘.
Tehát
γ≤180∘-2α.
Valóban, a talpponti háromszög legnagyobb szöge (180∘-2α) legalább akkora, mint az eredeti háromszög legnagyobb szöge. Egyenlőség akkor áll fenn, ha 2α+γ=α+β+γ. α=β≤γ<90∘, amiből 45∘<α=β≤60∘, 60∘≤γ<90∘ következik.
Az egyenlőség olyan egyenlő szárú háromszögekre teljesül, amelyekben a szárak által bezárt szög 60∘-nál nem kisebb hegyesszög.
 

 Hraskó András (Bp., I. István Gimn., II. o. t.)
 dolgozata alapján
 

Megjegyzések. 1. A talpponti háromszög legkisebb szöge legfeljebb akkora, mint az eredeti háromszög legkisebb szöge. Itt az egyenlőség (szükséges és elégséges) feltétele: 60∘≤β=γ<90∘.
2. Nem igaz az, hogy az egyenlőség bármilyen egyenlő szárú háromszögre érvényes! Mivel kiinduló feltevésünk szerint α≤β≤γ<90∘, ezért nem elegendő feltétel az α=β egyenlőség. Ha ugyanis α=β>γ lenne, akkor a talpponti háromszögben már nem a 180∘-2α nagyságú szög lenne a legnagyobb. A legtöbb hiányos dolgozat szerzője ezt a hibát követte el.