Kezdőlap


Feladat:	Gy.2097	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1983/május, 215 - 217. oldal		PDF \| MathML
Témakör(ök):	Kombinációk, Gyakorlat
Hivatkozás(ok):	Feladatok: 1983/január: Gy.2097

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a száz szám $a_{1} ≦ a_{2} ≦ ... ≦ a_{100}$ . Két esetet különböztetünk meg aszerint, hogy $a_{50} + a_{99}$ milyen előjelű. Mivel

\begin{matrix} a_{50} + a_{99} ≦ a_{51} + a_{99} ≦ ... ≦ a_{97} + a_{99} ≦ a_{98} + a_{99}, \end{matrix}

(1)

\begin{matrix} a_{50} + a_{99} ≦ a_{50} + a_{100} ≦ a_{51} + a_{1 o o} ≦ ... ≦ a_{98} + a_{100} ≦ a_{99} + a_{100}, \end{matrix}

(2)

ezért ha

a_{50} + a_{99} \geq 0

, akkor (1) és (2) alatt összesen

100

darab nemnegatív összeget soroltunk fel. Ezek között csak

a_{50} + a_{99}

szerepel kétszer, vagyis találtunk

99

olyan számpárt, ahol a két tag összege nem negatív.
Ha

a_{50} + a_{99} < 0

, akkor

\begin{matrix} a_{50} + a_{99} ≧ a_{49} + a_{98} ≧ ... ≧ a_{3} + a_{52} ≧ a_{2} + a_{51}, \end{matrix}

miatt ennek a 49 számpárnak az összege negatív. Ez az összeg viszont nem más, mint

S - (a_{1} + a_{100})

, ahol

S

jelöli a 100 szám összegét. A feltétel szerint

S = 0

, így ha

a_{50} + a_{99} < 0

, akkor

a_{1} + a_{100} > 0

. Ugyanakkor

\begin{matrix} a_{1} + a_{100} ≦ a_{2} + a_{100} ≦ ... ≦ a_{98} + a_{100} ≦ a_{99} + a_{100}, \end{matrix}

tehát most is találtunk 99 olyan számpárt, amelyben a két tag összege nem negatív.

II. megoldás. Ismeretes, hogy

2 n

csapat körmérkőzéses bajnokságát (minden csapat minden csapattal pontosan egyszer játszik)

2 n - 1

fordulóban le lehet bonyolítani úgy, hogy minden fordulóban minden csapat pontosan egy mérkőzést játszik.
A feladat állítása ebből a tételből következik. Képzeljük el ugyanis

100

csapatnak egy fenti,

99

fordulós bajnokságát. Ha egy fordulóban az

i

-edik és a

j

-edik csapat játszik egymással, akkor tekintsük az

a_{i} + a_{f}

összeget. Egy fordulóhoz

50

ilyen két tagú összeget rendeltünk, s minden két tagú összeg (ami egy mérkőzésnek felel meg) pontosan egy fordulóhoz tartozik. Az ugyanahhoz a fordulóhoz rendelt két tagú összegek összege

0

, hiszen ebben az

a_{1}, a_{2}, ..., a_{100}

alga számok mindegyike pontosan egyszer fordul elő. Így minden forduló mellett valamelyik két tagú összeg nem negatív, ami legalább annyi nemnegatív két tagú összeget jelent, ahány forduló van, azaz

99

-et.
A felhasznált tétel bizonyítása eljárást is ad a megfelelő beosztás elkészítésére. Legyen

a > 1

, és tekintsünk egy szabályos

2 n - 1

oldalú sokszöget. Az egyik csapatot ‐

C_{1}

‐ feleltessük meg a sokszög középpontjának, a többit pedig a sokszög csúcsainak. Tekintsük a

C_{1} C_{2}

sugarat, és a sokszög csúcsait összekötő átlók és oldalak közül azokat, amelyek merőlegesek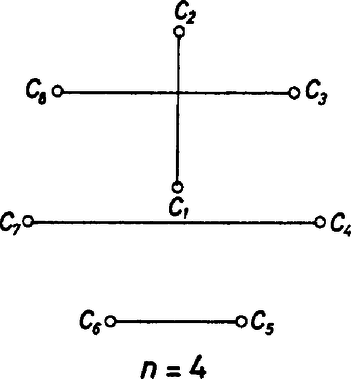

C_{l} C_{2}

-re (1. ábra).

A szakaszok a végpontjaikban álló csapatok közti mérkőzéseket tekintve éppen egy teljes forduló párosítását adják. Az

n

szakaszból álló alakzatot a sokszög középpontja körül

2 π / (2 n - 1)

egész számú többszöröseivel elforgatva összesen

2 n - 1

fordulóhoz jutunk. Minden fordulóban a korábbiaktól különböző mérkőzéseket kapunk, és az összes lehetséges mérkőzést megkapjuk, hiszen a sokszög valamennyi átlója, illetve oldala pontosan egy ilyen alakzatban szerepel.

Megjegyzések. 1. A két megoldás mindegyike szerint elég föltenni, hogy a

2 n

darab szám összege nem-negatív, már ebből is következik, hogy a közülük kiválasztandó számpárok között legalább

(2 n - 1)

-ben a tagok összege nem negatív. Ennél több nem-negatív párt már nem feltétlenül találunk, mert ha a számok egy kivételével negatívok, akkor csak az a

2 n - 1

összeg nem lesz nem negatív, amelyek egyik tagja az egyetlen pozitív elem.
Fölvethető, hogy

2 n + 1

szám esetén található-e mindig

2 n

olyan pár, amelyben a tagok összege nem negatív, ha a

2 n + 1

darab szám összege

\geq 0

. A válasz: igen, ha

n \geq 3

. Ugyanis ha a

2 n + 1

szám között van olyan

a_{i} < 0

és

a_{j}

, hogy

a_{i} + a_{j} \geq 0

, akkor a számok közül

a_{i}

-t elhagyva

2 n

számunk marad, melyek összege pozitív. A fenti állítás értelmében kiválasztható közülük

2 n - 1

,,nemnegatív pár'', ami az

(a_{i}, a_{j})

párral együtt éppen

2 n

.
Ha pedig minden olyan két tagú összeg negatív, amelyben a tagok ellenkező előjelűek, akkor mivel a számok összege

\geq 0

, a

2 n + 1

szám között legalább

n + 1

pozitív van. Ekkor legalább

(\binom{n + 1}{2}) = \frac{(n + 1) \cdot n}{2}

olyan pár van, amelyben a tagok összege nem negatív, s ez legalább

2 n

, ha

\geq 3

.
Az állítás

n = 2

és

n = 1

esetén nem is igaz:

n = 2

-re például a

(- 3;