Feladat: Gy.2096 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bujdosó László 
Füzet: 1983/október, 65 - 66. oldal  PDF  |  MathML 
Témakör(ök): Számelrendezések, Oszthatóság, Gyakorlat, Konstruktív megoldási módszer
Hivatkozás(ok):Feladatok: 1983/január: Gy.2096

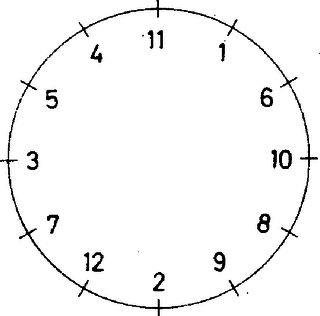
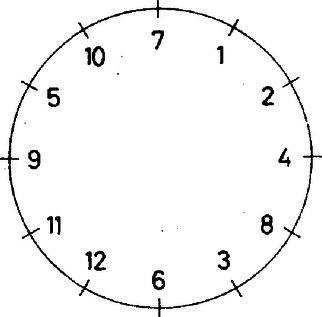
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megfelelő elrendezés látható az 1a és 1b ábrákon. További megfelelő felírásokat kapunk, ha a számokat fordított sorrendben helyezzük el a kör kerületén, vagy ha a köröket elforgatjuk. Bizonyítjuk, hogy más megoldás viszont nincs.

 
1a. ábra
 
1b. ábra
Egy tetszőleges 1≤a≤12 egész számra az a, 2a, 3a, ..., 12a számok 13-mal osztva különböző maradékokat adnak. Tegyük fel ugyanis, hogy ka és la 13-mal osztva mégis ugyanazt a maradékot adná (1≤l<k≤12). Ekkor k⋅a-l⋅a=(k-l)⋅a osztható lenne 13-mal. A jobb oldal törzstényezős felbontásában azonban nem szerepelhet a 13, mivel 0<a<13 és 0<k-l<13. Ez ellentmondás, tehát a maradékok között valóban nem lehetnek egyenlők. Így a maradékok között az összes 0 és 13 közötti egész szerepel.
A b2-ac kifejezés akkor osztható 13-mal, ha b2 és ac 13-mal osztva ugyanazt a maradékot adja. Ha adott a és b, akkor az előzők alapján pontosan egyféleképpen választhatunk ki az első 12 pozitív egész közül egy olyan c-t, amelyre ac ugyanazt a maradékot adja 13-mal osztva, mint b2. Ha most b-t választom a-nak, c-t pedig b-nek, akkor ezek ugyanígy meghatározzák a következő számot stb.
Végül is azt kapjuk, hogy ha a kör kerületére fölírunk két szomszédos számot, akkor ezek meghatározzák az összes többi szám sorrendjét is. Kezdjük a számok felírását az 1-gyel. Írjunk mellé egy másik számot. Az előzők alapján rendre felírjuk a soron következő összes többit is.
Ez a felírás nem lesz megfelelő, ha vagy a 12-edik szám előtt olyan számot kapunk, amely már szerepelt korábban, vagy ha a sorozat 13-adik tagja nem azonos az elsővel. Ha 1 mellett 3 vagy 9 szerepel, akkor a következő sorozatokat kapjuk: 1, 3, 9, 1 ill. 1, 9, 3, 1. Ezek tehát nem megoldások.

Ha 1 mellett 4 vagy 10 szerepel, akkor a sorozat így alakul: 1, 4, 3, 12, 9, 10, 1, ill. ennek megfordítottja. Ezek sem megoldások. Ha 1 mellé 5-öt vagy 8-at írunk, az 1, 5, 12, 8, 1, ill. 1, 8, 12, 5, 1 sorozatot kapjuk, ami szintén nem megoldás. 12 sem kerülhet 1 mellé, mivel így 1 másik szomszédja is 12 lenne. Tehát 1 mellé csak a 2, 6, 7, 11 számok valamelyikét írhatjuk, ezekben az esetekben viszont a már leírt megoldások valamelyikét kapjuk.
 

 Bujdosó László (Budapest, I. István Gimn., II. o.t.)
 

 

Megjegyzés. Az 1b ábrán az elrendezés 2 hatványaival indul: 1, 2, 4, 8, viszont a 16 helyett, ami túl nagy, a 3 áll. Ez azonban éppen 16-nak a 13-mal való osztásakor fellépő maradéka. Ez a továbbiakban is érvényes; megfigyelhető, hogy az 1b ábrán az 1-estől negatív irányban haladva az i-edik helyen éppen 2i-nek a 13-mal való osztásakor fellépő maradéka áll. Pozitív irányban haladva a számok a 7 hatványainak maradékai, az 1a ábrán pedig negatív irányban haladva a 6, pozitív irányban pedig a 11 hatványainak a 13-mal való osztáskor fellépő maradékai állnak.
A maradékokkal való számolás tulajdonságait felhasználva általában is könnyű megmutatni, hogy ha egy kör mentén egy adott szám hatványainak a 13-mal ‐ illetve tetszőleges p pozitív egésszel ‐ való osztásakor fellépő maradékai állnak, akkor bármely három egymást követő a, b, c számra b2-ac osztható 13-mal ‐ illetve p-vel. Az is belátható, hogy ha p prím ‐ a 13 az ‐ , akkor a fenti állítás megfordítása is igaz, vagyis a kitűzött feladatnak csak ilyen típusú megoldása lehet. Olyan r számot kell választani, amelyre r0, r1, r2, ..., rp-1 p-vel osztva kiadja az összes (p-1)-féle nem nulla maradékot. Az ilyen r számokat modulo p vett primitív gyököknek nevezik. A megoldás szerint p=13 esetén négy primitív gyök van, a 2, a 6, a 7 és a 11. Általában is minden prímszámhoz található primitív gyök.