Feladat: Gy.2094 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1983/szeptember, 16 - 17. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikai leszámolási problémák, Legnagyobb közös osztó, Gyakorlat, Sakk
Hivatkozás(ok):Feladatok: 1983/január: Gy.2094

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Minden olyan mező, amelyen az átló keresztülhalad, egy szakaszt metsz ki az átlóból. Egy ilyen szakasz két végpontja az átló és a mező kerületének két metszéspontja. Azt kell tehát megszámolnunk, hogy a mezők határolóegyeneseivel alkotott metszéspontok hány szakaszra osztják fel az átlót.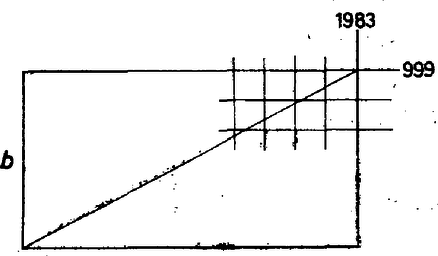
A függőleges egyenesek száma 1984, ez 1984 metszéspontot jelent. Az 1000 darab vízszintes egyenes 1000 pontban metszi az átlót, ezek között azonban lesznek olyan metszéspontok is ‐ például a legelső vagy az utolsó ‐, amelyeken függőleges egyenesek is áthaladnak. Az ilyen pontokat ‐ tehát azokat a csúcspontokat, amelyeken az átló keresztülhalad ‐ kétszer számoltuk.
Ha az átló egy csúcsponton halad keresztül, akkor a létrejövő téglalap hasonló az eredetihez, és ha a mező oldala egységnyi, akkor oldalai szintén egészek.

 

 
Oldalaira fennáll, hogy
ab=1983999és1≤a≤1983.(1)
Megfordítva, minden olyan a, b egész számokból álló számpárhoz, melyre (1) teljesül, tartozik egy, az ábrán látható téglalap, vagyis egy csúcs, amelyen a sakktábla átlója áthalad.
Mivel 1983 és 999 legnagyobb közös osztója 3, azért (1) alapján ab=661333, és ez az alak tovább már nem egyszerűsíthető. Ez azt jelenti, hogy a egész számú többszöröse 661-nek, b pedig 333-nak. Másrészt a≤1983, ezért (1)-nek pontosan 3 megoldása van, mégpedig
a=661,b=333;a=1322,b=666a=1983,b=999.
Öszesen tehát négy csúcsponton halad keresztül az átló, ezek közül kettő a sakktáblának is csúcsa, a másik kettő pedig az átló harmadolópontjai.
A mezők határolóegyenesei tehát 1984+1000-4=2980 pontban metszik az átló egyenesét. A létrejövő szakaszok száma ennél 1-gyel kevesebb, vagyis a sakktábla átlója 2979 mezőn halad keresztül.
 
Megjegyzések. 1. A megoldás során azt is megmutattuk, hogy ha a sakktábla oldalai relatív prímek, akkor a sakktábla átlója egyetlen mező csúcsán sem halad át a tábla belsejében.
2. A bizonyításból következik, hogy egy k×n oldalú sakktábla átlója (k+n+1)-d mezőn halad keresztül, ahol d a k és n számok legnagyobb közös osztója.