Feladat: Gy.2082 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1983/október, 64 - 65. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Gyakorlat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1982/november: Gy.2082

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel ABCD konvex, azért az AB oldalegyenesnek és a CD szakasznak nincs közös pontja ‐, így P és Q a CD egyenesnek ugyanazon az oldalán van. Az AQ=QC feltétel miatt az A pontot a PQ egyenesből a Q középpontú, QC sugarú kA kör metszi ki. Hasonlóan a B pontot a PQ egyenesből a P középpontú, PD sugarú kB kör metszi ki.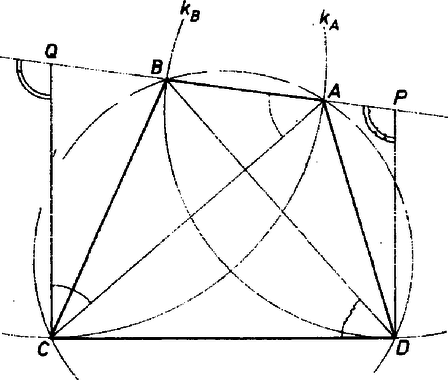

Mivel CD érintője kA-nak és kB-nek, ezért ezek a metszéspontok CD-nek ugyanarra a partjára esnek, ahol P és Q található. Ahhoz, hogy ABCD konvex (és ne hurkolt) négyszög legyen, szükséges, hogy AB→ vektor iránya megegyezzen a PQ→ vektor irányával. Ezért A a kA-nak és PQ-nak P felé eső metszéspontja, B pedig kB-nek és PQ-nak Q felé eső metszéspontja.
Annak igazolása, hogy az ABCD konvex négyszög húrnégyszög, elegendő belátnunk, hogy az A és D pontokból a BC szakasz egyenlő szög alatt látszik.
A kB kör BD ívéhez tartozó középponti szög kétszerese a húrhoz tartozó érintőszögnek:
QPD∢=BPD∢=2⋅BDC∢.
A QAC háromszögben QA=QC, tehát
2⋅BAC∢=2⋅QAC∢=QAC∢+QAC∢=180∘-CQP∢.
Végül kihasználva, hogy PQCD derékszögű trapéz, azaz CQP∢+QPD∢=180∘, kapjuk a kívánt BDC∢=BAC∢ egyenlőséget.