Kezdőlap


Feladat:	Gy.2078	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dringó László
Füzet:	1983/május, 209 - 210. oldal		PDF \| MathML
Témakör(ök):	Paraméteres egyenletrendszerek, Egyenletrendszerek, Kör egyenlete, Gyakorlat
Hivatkozás(ok):	Feladatok: 1982/november: Gy.2078

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha $a < 0$ , akkor egyik egyenletrendszerünknek sincs megoldása, a két megoldáshalmaz tehát azonos ‐ az üres halmaz ‐ ilyenkor tehát I. és II. ekvivalensek.
A továbbiakban legyen $a \geq 0$ . II. második egyenlete azt mondja ki, hogy $x + y$ egész szám. A két egyenletrendszer tehát az $a$ -nak olyan értékeire ekvivalens, amikor ez az egész szám a O. Így $a$ -nak azokat az értékeit kell kizárnunk, melyekre az $x^{2} + y^{2} = a$ feltétel mellett $x + y$ fölvehet $0$ -tól különböző egész értéket is.
Vezessük be az $x + y = m$ jelölést ( $m$ egész), és vizsgáljuk meg, hogyan függenek II. megoldásai $a$ -tól és $m$ -től. Az $x = m - y$ összefüggést az első egyenletbe helyettesítve, rendezés után

\begin{matrix} 2 y^{2} - 2 m y + m^{2} - a = 0 \end{matrix}

(2)

adódik.
Az I. és II. egyenletrendszer pontosan akkor ekvivalens, ha (2) semmilyen

y

-ra nem teljesül, ha

m

0-tól különböző egész szám, vagyis ha (2) diszkriminánsa,

4 (2 a - m^{2})

, negatív

m

-nek ilyen értékeire.
Ha

m \neq 0

és egész, akkor

m^{2}

legalább 1. A diszkrimináns tehát pontosan akkor lesz minden, 0-tól különböző

m

egész számra negatív, ha

2 a < 1

, azaz

a < \frac{1}{2}

Dringó László (Budapest XI., Petőfi S. Ált. Isk., 8. o. t.)

II. megoldás. Ismét feltesszük, hogy

a \geq 0

és ábrázoljuk a derékszögű koordináta-rendszerben az egyes egyenletrendszerek megoldásait. Azok a pontok, melyeknek koordinátáira

x^{2} + y^{2} = a

teljesül, egy origó középpontú,

\sqrt[]{a}

sugarú körvonalon helyezkednek el. Az

x + y = m

feltételnek eleget tevő pontok pedig egymással párhuzamos egyeneseken.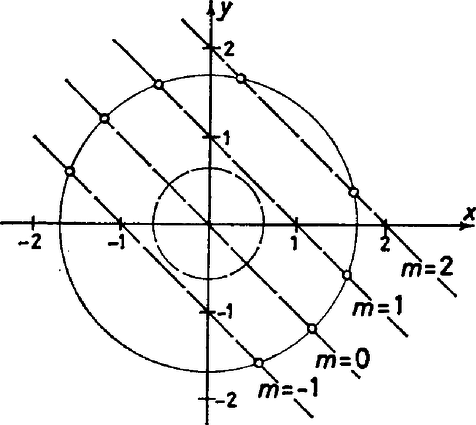

Mivel

a \geq 0

, a két egyenletrendszer

a

-nak azokra az értékeire ekvivalens, amelyekre a

\sqrt[]{a}

sugarú, origó középpontú körnek csak az

m = 0

értékhez tartozó egyenessel van közös pontja, vagyis a kör az

m = 1

, illetve az

m = - 1

értékekhez tartozó

x + y = 1

, illetve

x + y = - 1

egyenletű egyenesek által határolt tartomány belsejében helyezkedik el.
Az origó épp felezi e két egyenes távolságát, ami

\sqrt[]{2}

, így a kapott feltétel pontosan akkor teljesül, ha a kör sugara kisebb, mint

\sqrt[]{2} / 2

, vagyis

a < 1 / 2