Kezdőlap


Feladat:	Gy.2059	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	1982/december, 210 - 211. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Tengelyes tükrözés, Szögfelező egyenes, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1982/május: Gy.2059

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $100^{\circ}$ -os szög az egyenlő szárú háromszögben csak szárszög lehet, s így a háromszög alapon fekvő szögei $40^{\circ}$ -osak. Legyen $E$ az $A B$ oldalnak az a pontja, amelyre $A E = A D$ . Ilyen pont van, hiszen $A D B ∢ > A C B ∢ >$ $> D B A ∢$ , amiből következik hogy $A B > A D$ . Így eredeti állításunk ekvivalens a következővel: $A E + D C = A B$ . Elegendő tehát a $D C = E B$ bizonyítása. Ezt két lépésben látjuk be.
Először az $A E D$ egyenlő szárú háromszöget vizsgáljuk. Itt $A D E ∢ = A E D ∢ = 80^{\circ}$ , így $D E B ∢ = 100^{\circ}$ . Mint tudjuk, $D B E ∢ = 40^{\circ}$ , s emiatt $E D B ∢$ ugyancsak $40^{\circ}$ -os, azaz

\begin{matrix} E B = E D . \end{matrix}

(1)

Második lépésként tükrözzük a

C

pontot az

A D

szögfelezőre. Ennek

C'

tükörképe nemcsak az

A B

oldalon van rajta, hanem az

A E

szakaszon is, hiszen

D C' A ∢ > D E A ∢

. A tükrözés miatt

D C' B ∢ = 180^{\circ} - A C' D ∢ = 180^{\circ} -

- A C D ∢ = 80^{\circ}

, és mivel

A E D ∢ = 80^{\circ}

, kapjuk, hogy

\begin{matrix} E D = D C' . \end{matrix}

(2)

Az (1), (2) és a tükrözés alapján kapott

D C' = D C

egyenlőségeket összevetve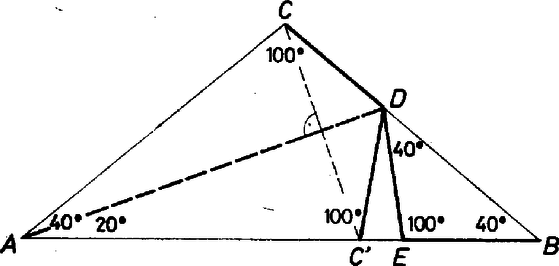

\begin{matrix} E B = E D = D C' = D C \end{matrix}

s ezzel igazoltuk az állítást.

II. megoldás. Az első megoldáshoz hasonlóan mérjük fel az

A E = A D

távolságot az

A B

oldalra. A

B D E

háromszög hasonló az

A B C

háromszöghöz, hiszen megfelelő szögeik egyenlők. Tudjuk továbbá, hogy az

A D

szögfelező a közrezáró oldalak arányában osztja a

B C

oldalt. Ezekből azt kapjuk, hogy

\begin{matrix} E D : D B = C A : A B = C D : D B \end{matrix}

amiből

E D = C D

következik. Mivel

E D = E B

és

A E = A D

, ezért

\begin{matrix} A B = A E + E B = A D + C D, \end{matrix}

amint azt bizonyítani akartuk.
(B. G.)