Feladat: Gy.2027 Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Bene László 
Füzet: 1982/november, 136 - 138. oldal  PDF  |  MathML 
Témakör(ök): Magasságvonal, Körülírt kör, Gyakorlat, Síkgeometriai bizonyítások, Thalesz tétel és megfordítása
Hivatkozás(ok):Feladatok: 1982/január: Gy.2027

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az hogy két kör merőlegesen metszi egymást, azt jelenti, hogy a metszéspontjaikban húzott érintőik merőlegesek egymásra, vagy ami ezzel egyenértékű, hogy a közös pontjukban húzott sugaraik merőlegesek egymásra. Ezt fogjuk bizonyítani.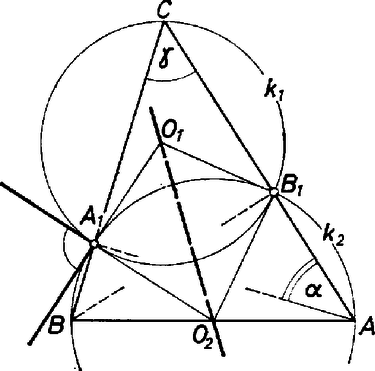
Az AA1⊥BC és BB1⊥AC, azaz A1, B1 pontok rajta vannak az AB szakasz Thalész körén, k2-n. Továbbá azt is tudjuk, hogy A1, B1 a k1 körnek is pontja. Jelöljük k1 középpontját O1-gyel, k2-ét O2-vel. Nyilvánvaló, hogy O1A1O2∢=O1B1O2∢, hiszen ezek egymás tükörképei az O1O2 centrálisra. Legyen BCA∢=γ és A1AC∢=α. Mivel a háromszög hegyesszögű, α<BAC∢<90∘, és γ<90∘ miatt mindkettő ugyanannak a derékszögű háromszögnek a szöge és α+γ=90∘. A k1 körben az A1O1B1∢=2A1CB1∢=2γ, ugyanazon ívhez tartozó kerületi és középponti szögek. A k2 körben hasonlóan A1O2B1∢=2A1AB1∢=2α, hiszen A1, B1 az AB átmérő ugyanazon oldalára esnek.

 

1. ábra
 

Ezekből következik, hogy az A1O1B1O2 deltoidban
O1A1O2∢+O2B1O1∢=360∘-(2α+2γ)=180∘,
tehát mindegyikre külön-külön 90∘ jut, amint azt bizonyítani akartuk.
 

II. megoldás. Húzzuk meg az ABC háromszög harmadik magasságvonalát is, talppontját jelöljük C1-gyel. A CA1B1 pontokon átmenő k1 kör átmegy a háromszög M magasságpontján is, megegyezik a CM szakasz Thalész körével. A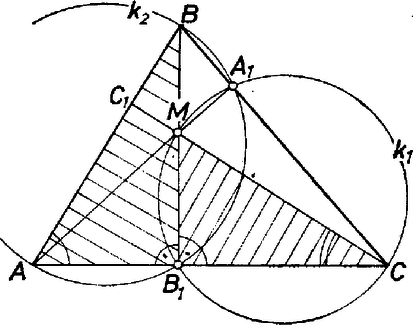
B1AB▵∼C1AC▵
mindkettő derékszögű és az A csúcsnál levő szögük közös. Mivel a háromszög hegyesszögű, M belső pont.
 

2. ábra
 

De akkor az ABB1 háromszög hasonló az MCB1 háromszöghöz is, mégpedig úgy, hogy B1 pont körül 90∘-kal megfelelő irányba elforgatva, hasonló helyzetbe hozhatók. Ez a 90∘-os forgatás a k2 kört is elforgatja, mégpedig úgy, hogy az k1-nek a B1-ből kicsinyített képe lesz. Tehát eredetileg a két kör merőlegesen metszette egymást.
 

 Bene László (Győr, Czuczor G. Bencés Gimn., II. o. t.)
 

III. megoldás. Emeljünk merőlegest A-ban az AC, B-ben a BC egyenesre. Ezek az egyenesek metszik egymást, hiszen az AC, BC egyenesek is metszik egymást. Jelöljük a metszéspontot F-fe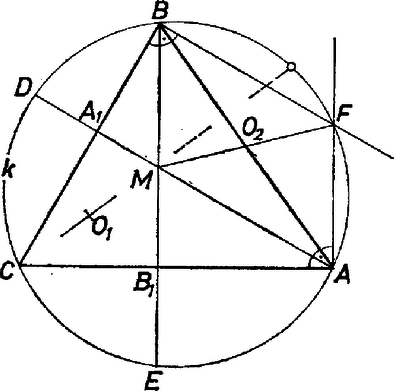l.
 

3. ábra
 

Thalész tétele szerint F az ABC háromszög köré írható k körben a C-vel átellenes pont. Ha az F-et meghatározó egyeneseket az AB szakasz O2 felezőpontjára tükrözzük, definíciójuk szerint az ABC háromszög A-n, B-n átmenő magasságvonalait kapjuk. Tehát F-nek O2-re vonatkozó tükörképe az ABC háromszög M magasságpontja. (Más szavakkal elmondva ugyanezt), azt kapjuk, hogy k-nak az AB szakasz O2 felezőpontjára vonatkozó tükörképe átmegy M-en. Mivel AB a k húrja, ez utóbbi tükrözés eredménye nem változik meg, ha magára az AB szakaszra tükrözünk.
Ismét fordítva egyet az állításunkon, azt kapjuk, hogy M-nek az AB-re vonatkozó tükörképe is rajta van k-n. Mivel ebben az állításban az AB oldalnak nincs kitüntetett szerepe, alkalmazhatjuk az AC, BC oldalakra is. Jelöljük a kapott tükörképeket E-vel, D-vel. Ezekből, a CF szakasz derékszög alatt látszik, hiszen CF a k átmérője. Mivel a C, D, E, F pontokat M-mel összekötő szakaszok felezőpontja épp az O1, A1, B1, O2 pont lesz, ezzel beláttuk, hogy az O1O2 szakasz az A1, B1 pontokból valóban derékszög alatt látszik.
 

Megjegyzés: A III. megoldásban nem használtuk fel, hogy az ABC háromszög hegyesszögű. A megoldás során az ABC háromszög köré írt k kört az M centrumból felére kicsinyítettük. Láttuk, hogy az új körön rajta vannak az eredeti háromszög oldalfelező pontjai, magasságvonalának a talppontjai, és a magasságpontot a csúcsokkal összekötő szakaszok felezőpontjai. Ez az ún. Feuerbach-kör, amelyet a k-ból általában az ABC háromszög S centrumára vonatkozó hasonlósággal szokás előállítani.