Kezdőlap


Feladat:	Gy.2026	Korcsoport: 14-15	Nehézségi fok: könnyű
Füzet:	1982/november, 135 - 136. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Négyszögek geometriája, Gyakorlat, Magasságvonal, Középvonal
Hivatkozás(ok):	Feladatok: 1982/január: Gy.2026

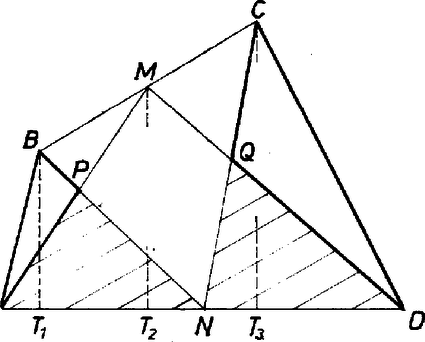
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az eredeti állítás helyett lássuk be a következőt: az $A M D$ háromszög területe egyenlő az $A B N$ és $N C D$ háromszögek területének összegével. A két állítás egyenértékű (ekvivalens). Ugyanis ha két egyenlő területű síkidomból elhagyjuk a közös részüket, akkor a megmaradó részek területe is egyenlő lesz. Márpedig az $A M D$ és $(A B N + N C D)$ síkidomokból közös részüket az $A P N$ és $N Q D$ háromszögeket elhagyva egyrészt az $M P N Q$ négyszög, másrészt az $A B P$ és $C Q D$ háromszögek maradnak.

Most már csak azt kell belátnunk, hogy

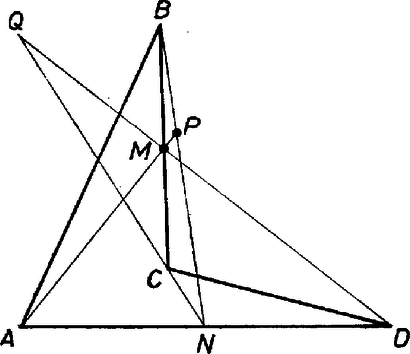
\begin{matrix} A M D ter = A B N ter + N C D ter \end{matrix}

(1)

Húzzuk meg mindhárom háromszögnek az

A D

oldalhoz tartozó magasságát. A magasságok talppontjait jelöljük rendre

T_{1}

T_{2}

és

T_{3}

-mal. Így (1) jobb oldala a következő alakba írható:

\begin{matrix} \frac{A D}{2} \cdot \frac{B T_{1}}{2} + \frac{A D}{2} \cdot \frac{C T_{3}}{2} = \frac{A D}{2} \cdot \frac{B T_{1} + C T_{3}}{2} = \frac{A D}{2} \cdot M T_{2}, \end{matrix}

hiszen

T_{1} B C T_{3}

egy derékszögű trapéz, s mivel

N

felezi

A D

-t,

A N = N D = \frac{A D}{2}

, és

M

felezi

B C

-t, így

M T_{2}

középvonal és

M T_{2} = \frac{B T_{1} + C T_{3}}{2}

. Ezzel igazoltuk az állítást.
Az állítás nyilván nem igaz, ha a négyszög konkáv. Ekkor ugyanis vagy az

A B N

vagy az

N C D

háromszög nem tartalmazza az

A P N

, ill.

N Q D

háromszöget, pl. ábránkon ez utóbbi áll fenn.