Kezdőlap


Feladat:	Gy.2021	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/október, 67 - 68. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1981/december: Gy.2021

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A B C$ a keresett háromszög, és jelöljük $P$ -nek az egyes csúcsoktól mért távolságát a megfelelő kisbetűvel. Az $A B C$ háromszög a $P$ körül szabadon forgatható, és tetszőleges, a $P$ -n átmenő tengelyre tükrözhető, hiszen ezek a transzformációk az $A B C$ háromszög szabályosságát és a csúcsok $P$ -től mért távolságait változatlanul hagyják. Válasszuk az $A B C$ háromszög körüljárását pozitívnak és forgassuk el $60^{\circ}$ -kal a háromszöget és benne a $P$ pontot $A$ körül. Ez a forgatás $B$ -t $C$ -be viszi, $C$ és $P$ új helyzetét jelöljük $D$ -vel, illetve $Q$ -val. A forgatás miatt $C Q = B P$ , és az $A P Q$ háromszög szabályos. Tehát a $C P Q$ háromszög oldalai rendre egyenlőek az adott szakaszokkal: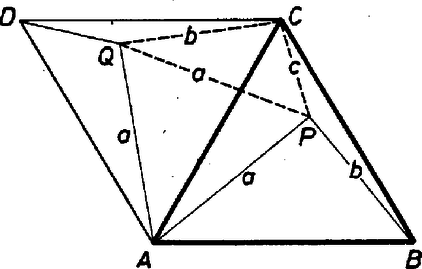

C P = c

C Q = b

P Q = a

. Mivel olyan háromszöget keresünk, amelyikben

P

belső pont, az

a

b

c

oldalakkal megszerkesztett háromszög csak akkor ad megoldást, ha a szögei kisebbek

120^{\circ}

-nál, hiszen a

P C Q

szög benne van a

120^{\circ}

-os

B C D

szögben, a

Q P C

P Q C

szögeket pedig úgy kapjuk a

180^{\circ}

-nál kisebb

A P C

A Q C

szögekből, hogy elvesszük belöle a

60^{\circ}

-os

A P Q

A Q P

szögeket.
A szerkesztés menete tehát a következő. Szabadon megválaszthatjuk a

P

-től

c

távolságra levő

C

pontot és a

P C

szakasz valamelyik oldalán megszerkesztjük a

P

középpontú

a

sugarú és

C

középpontú,

b

sugarú körök

Q

metszéspontját. A keresett háromszög csak akkor létezik, ha a

P Q C

háromszög létrejön, és szögei

120^{\circ}

-nál kisebbek. Ha ez így van, a

P Q

szakasz

C

-vel átellenes oldalára rajzolt

P Q A

szabályos háromszög harmadik csúcsa a keresett háromszög következő csúcsa, és

B

-t az az

A

körüli

60^{\circ}

-os forgatás adja

C

-ből, amelyik

Q

-t

P

-be viszi. A forgatás miatt

A B C

valóban szabályos háromszög. Mivel a

P Q C

háromszög szögei

120^{\circ}

-nál kisebbek,

A

P C Q

szögtartományban van, az

A C

és

P Q

szakaszok metszik egymást. Így a

Q

-t

P

-be vivő forgatás

C

-t túlforgatja az

A P

irányon,

P

benne lesz a

B A C

szögtartományban. Az

A P C

A P B = A Q C

szögek kisebbek

180^{\circ}

-nál, és az összegük

\begin{matrix} A P C ∢ + A P B ∢ = A P Q ∢ + Q P C ∢ + A Q P ∢ + P Q C ∢ = \\ = 120^{\circ} + 180^{\circ} - P C Q ∢ \end{matrix}

miatt nagyobb

180^{\circ}

-nál, hiszen a

P C Q

szög kisebb

120^{\circ}

-nál. Tehát a

P B C

szög kisebb

180^{\circ}

-nál,

P

valóban belső pontja az

A B C

háromszögnek. A csúcsoktól mért távolsága pedig rendre egyenlő, az adott szakaszokkal, hiszen

P A = P Q

P B = C Q

a szerkesztés miatt.

Megjegyzések. 1. A cosinus tétel alapján látható, hogy ha az adott

a

b

c

szakaszok közül mondjuk a

c

a legnagyobb, akkor a szerkeszthetőség feltétele

\begin{matrix} c^{2} < a^{2} + a b + b^{2} . \end{matrix}

2. Megoldhatjuk úgy is a feladatot, hogy felveszünk egy a keresett

A B C

háromszöghöz hasonló tetszőleges szabályos

A' B' C'

háromszöget, és benne a

P

-hez hasonló helyzetű

P'

pontot keressük az

\begin{matrix} A' P' : B' P' = a : b, B' P' : C' P' = b : c \end{matrix}

arányoknak megfelelő Apolloniusz‐körök metszéseként. Aztán alkalmas hasonlósággal az egészet átépítjük a

P

pont köré.
3. Ha nem kötjük ki azt, hogy

P

A B C

háromszög belső pontja legyen, az eredeti szerkesztés során

A

helyett a

P Q

-ra vonatkozó tükörképét is vehetjük. Ebben az esetben csak az a szerkeszthetőség feltétele, hogy az adott

a

b

c

szakaszokkal háromszög legyen szerkeszthető, és általában két, különböző méretű

A B C

háromszöget kapunk.