Kezdőlap


Feladat:	Gy.2014	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1982/május, 215 - 216. oldal		PDF \| MathML
Témakör(ök):	Számelrendezések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1981/december: Gy.2014

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje a csúcsokat rendre $A$ , $B$ , $C$ , $D$ , $E$ , a melléjük írt számokat pedig ugyanebben a sorrendben 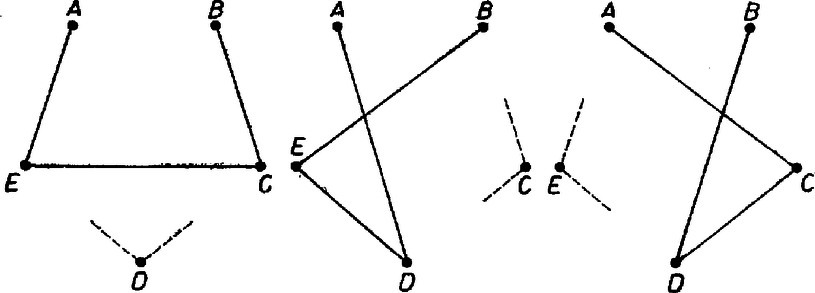$a$ , $b$ , $c$ , $d$ és $e$ .
Három összeg egész voltáról nincs még tudomásunk, feltehető, hogy ezek egyike az $A B$ élre írt $(a + b)$ . Megmutatjuk, hogy $(a + b)$ is egész.
Az ötszög $A B$ élén kívüli többi élt és átlót soroljuk három darab hármas csoportba úgy, hogy az egyes csoportokba kerülő élek mentén, minden élen egyszer haladva át, $A$ -ból $B$ -be jussunk. Ez a felosztás látható az ábrán.

Mivel a kilenc él közül csak

2

-ről nem tudjuk, hogy egész szám áll-e rajta, így van olyan élsorozat, amelynek mindhárom élére egész számot írtunk. Legyen ez például az

A D

D E

E B

. Ez azt jelenti, hogy az

(a + d), (d + e), (e + b)

összegek egészek. Egész számok összege és különbsége is egész, így

a + b =

= (a + d) + (e + b) - (d + e)

valóban egész szám.
A bizonyítás alkalmas betűzéssel a kérdéses három él bármelyikére elmondható, így az állítást igazoltuk.

Megjegyzések. 1. Az nem igaz, hogy maguk a számok is egészek, hisz nyilván megfelelő kitöltést kapunk, ha minden csúcshoz

\frac{1}{2}

-et írunk. Könnyen látható azonban, hogy minden szám kétszerese egész, hisz pl.

2 a = (a + b) + (a + c) - (b + c)

.
2. Ha csak hat összegről tudjuk, hogy egész, akkor lehetséges, hogy a továbbiak nem azok. Ilyen kitöltést kapunk, ha egy csúcsra törtszámot, a további négyre pedig egész számot írunk.