Feladat: Gy.2006 Korcsoport: 14-15 Nehézségi fok: könnyű
Füzet: 1982/május, 211 - 212. oldal  PDF  |  MathML 
Témakör(ök): Egyenletek grafikus megoldása, Abszolútértékes egyenletek, Egészrész, törtrész függvények, Gyakorlat, Esetvizsgálat
Hivatkozás(ok):Feladatok: 1981/november: Gy.2006

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Oldjuk meg az alábbi egyenletet:

1-|x+1|=[x]-x|x-1|.(1)

I. megoldás. A tört nevezője nem lehet 0, ezért x≠1. A továbbiakban három esetet különböztetünk meg aszerint, hogy az egyes abszolút érték jelek hogyan bonthatók fel.
Ha x>1, akkor |x+1|=x+1,|x-1|=x-1, és rendezés után (1) így alakul:
[x]=2x-x2.(1a)

Mivel x>1, ezért [x]≥1 is teljesül, így (1a) szerint 2x-x2≥1, ahonnan rendezés után (x-1)2≤0 adódik. Ez csak akkor teljesül, ha x=1, amit viszont kizártunk.
Ha -1≤x<1, akkor |x+1|=x+1,|x-1|=1-x, így most az
[x]=x2(1b)
egyenletet kapjuk. Az adott intervallumban [x] értéke -1, vagy 0, így csak x2=0 lehetséges, hiszen x2 nem lehet negatív. Ekkor x=0, ami valóban megoldása (1)-nek.
Ha x<-1, akkor |x+1|=-(x+1),|x-1|=1-x, tehát most
[x]=2-x2(1c)
adódik.
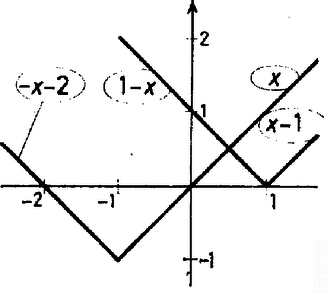
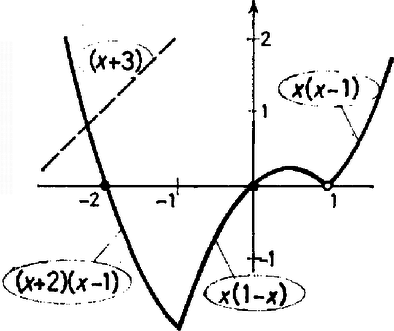
Mivel [x]>x-1, ezért (1c)-ből x-1<2-x2, ahonnan x<-1 miatt x>-13+12>-3. Így [x] szóba jövő értékei -2, vagy -3.
Ha [x]=-2, akkor (1c) alapján x=-2, amelyre valamennyi feltétel teljesül, ha pedig [x]=-3, akkor x=-5, ami ugyancsak megoldás.
Így egyenletünknek három megoldása van. Ezek: -5,-2 és 0.
 

II. megoldás. Szorozzuk meg (1) mindkét oldalát -|x-1|-gyel, és ábrázoljuk a koordináta-rendszerben a kapott
|x-1|(|x+1|-1)=x-[x](2)
egyenlet két oldalán álló függvényeket.
 
1. ábra
 
2. ábra
 
3. ábra

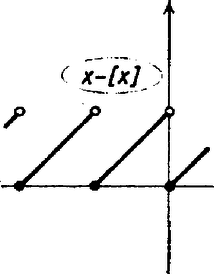
A bal oldalon álló szorzat első tényezője x≤-1 mellett (-x-2)-vel, x>-1 mellett x-szel egyenlő, a második tényező x≤1 mellett (1-x)-szel, x>1 mellett (x-1)-gyel egyenlő (1. ábra). Így a bal oldal értéke rendre (2. ábra)
(x+2)(x-1),x(1-x),vagyx(x-1)
aszerint, hogy
x≤-2,x≤1,vagyx>1.

A jobb oldalon álló függvényt x tört részének hívják, és értéke tetszőleges x mellett 0 és 1 között van, hiszen [x] nem lehet nagyobb x-nél, és nem lehet kisebb (x-1)-nél (3. ábra). Emiatt x értékét (-∞) felől növelve először -3 és -2 között lehet egyenlő a két függvény értéke, hiszen x<-3 mellett x+2< <-1,x-1<-4, így (x+2)(x-1)>4. Ha -3≤x<-2, akkor [x]=-3, tehát (2) ekvivalens az
(x+2)(x-1)=x+3
egyenlettel, amiből a műveletek elvégzése után az x2=5 egyenletet kapjuk. Ennek az adott szakaszon x=-5 a gyöke, ami (1)-nek is gyöke. Tovább menve x=-2 is gyök, viszont -2<x<0 mellett a bal oldal értéke negatív, tehát ezen a szakaszon nincs gyök. A szakasz x=0 végpontja ismét gyök, és 0<x<1 mellett a bal oldal értéke kisebb x-nél, így itt nincs további gyök. Az x=1 végpont (2)-nek ugyan gyöke, de (1)-nek nem. További gyök nincs, mert x>1 mellett a bal oldal értéke nagyobb (x-1)-nél, és ez nagyobb a jobb oldal értékénél.