Kezdőlap


Feladat:	Gy.1979	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/január, 8 - 9. oldal		PDF \| MathML
Témakör(ök):	Feuerbach-kör, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1981/április: Gy.1979

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C D$ négyszög $A$ -nál és $C$ -nél levő szöge Thalész tétele miatt derékszög. A $P$ , $Q$ , $R$ metszéspontok akkor és csak akkor léteznek, ha az $A B C D$ négyszög nem téglalap. Ezt a továbbiakban fel is tételezzük, más szóval azt, hogy $C$ a körnek nem $A$ -val átellenes pontja. Feltesszük még, hogy a $B$ és $D$ pontok közül $D$ van a kisebbik $A C$ íven. Ezt megtehetjük, mivel $B$ és $D$ szerepe felcserélhető. A $B P$ egyenesnek az $A$ , $B$ pontokon kívül nem lehet a körrel további metszéspontja, így $C$ nem lehet ezen az egyenesen, és emiatt a $P$ pont sem lehet a $B R$ egyenesen.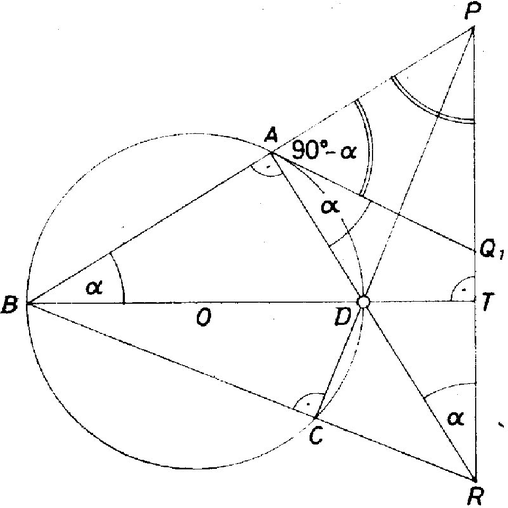
Minthogy a $C D$ és $A D$ egyenesek a $B P R$ háromszög magasságvonalai, $D$ e háromszög magasságpontja. Így a $B P R$ háromszögnek a $B D$ egyenes is magasságvonala. Jelöljük a $B D$ és $P R$ egyenesek metszéspontját $T$ -vel, a körhöz $A$ -ban húzott érintő és $P R$ metszéspontját $Q_{1}$ -gyel, az $A B D$ szöget pedig $α$ -val.
Az $A R Q_{1}$ és $A B D$ szögek egyenlők, mert mindkettő pótszöge az $A P Q_{1}$ szögnek. Az $A D$ íven nyugvó $Q_{1} A R$ érintő szárú kerületi szög ugyancsak egyenlő az $A B D$ szöggel, amely ugyanazon az $A D$ íven nyugvó kerületi szög. Az $A R Q_{1}$ háromszög tehát egyenlő szárú: $A Q_{1} = R Q_{1}$ .

A P Q_{1}

háromszög szintén egyenlő szárú, mivel az

A P

oldalon fekvő szögei egyenlők (

P A Q_{1} ∢

és

A P Q_{1} ∢

is pótszöge

α

-nak), így

A Q_{1} = P Q_{1}

.
Mindebből következik, hogy

Q_{1}

P R

szakasz felezőpontja. Hasonló módon belátható, hogy a

P B

szakaszt a körhöz

C

-ben húzott érintő is a felezőpontjában metszi. Tehát e felezőpont egyben a két érintő metszéspontja.

Megjegyzések. 1. Megoldásunk szerint a

B D

szakasz

O

felezőpontja, és a

Q

pont által meghatározott

O Q

szakasz az

A

C

T

pontokból derékszög alatt látszik, tehát az

O Q

feletti Thalész kör átmegy az

A

C

T

pontokon. Ez a kör a

B P R

háromszög ún. Feuerbach‐köre.
2. Amint azt sokan észrevették, a bizonyítandó állítás egy speciális esete Pascal tételének, amely szerint egy közönséges kúpszeletbe írt hatszög átellenes oldalpárjai vagy egy egyenes három pontjában metszik egymást, vagy páronként párhuzamosak, vagy a hatszög egyik átellenes oldal párját alkotó oldalai párhuzamosak a másik két átellenes oldalpár metszéspontjai által meghatározott egyenessel. (A tétellel kapcsolatos kérdéskör részletes tárgyalása megtalálható például Hajós György: Bevezetés a geometriába c. művében.)
A közönséges kúpszelet szerepét gyakorlatunkban a

B D

átmérőjű kör játssza, a beírt hatszögét pedig az

A B C D

négyszög, amelynek

A

és

C

csúcsát olyan csúcsoknak tekintjük, ahol két‐két csúcspont egybeesik. (Egybeeső csúcsokat összekötő oldalegyeneseknek a kör érintői felélnek meg.)
A Pascal‐tételt felhasználó bizonyításokat kellő magyarázattal helyes megoldásnak fogadtuk el. (R. Zs.)