| Feladat: | Gy.1965 | Korcsoport: 16-17 | Nehézségi fok: könnyű |
| Megoldó(k): | Baráti Ákos | ||
| Füzet: | 1981/december, 206 - 207. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Geometriai egyenlőtlenségek, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1981/február: Gy.1965 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először azt látjuk be, hogy egy háromszög belsejében fekvő tetszőleges paralelogrammához mindig található olyan másik paralelogramma, amelynek területe nem kisebb az eredetiénél, és amelynek mind a négy csúcsa a háromszög kerületére esik. Ez utóbbiról még azt is megkövetelhetjük, hogy egyik csúcsa essen egybe a háromszög valamelyik csúcsával. 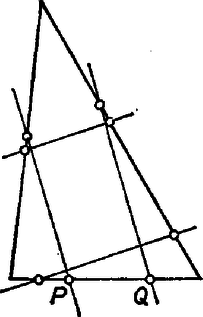 1. ábra Két ilyen pont által határolt szakaszhoz mint oldalhoz olyan paralelogramma illeszthető, amelyet a háromszög tartalmaz, és amely az eredeti paralelogrammával egyenlő területű. Ezt a 2. ábrán látható területdarabolás bizonyítja. 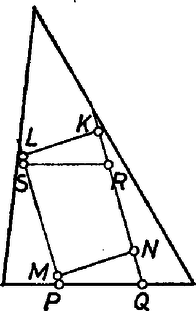 2. ábra A paralelogrammát az négyszöggel kiegészítjük, majd az így kapott négyszögből elvesszük az -vel egybevágó négyszöget. a kívánt paralelogramma. Ehhez nem nehéz olyan paralelogrammát találni, amely nála nem kisebb területű, és amelynek mind a négy csúcsa a háromszög kerületén van úgy, hogy közülük egy a háromszögnek is csúcsa (3. ábra). 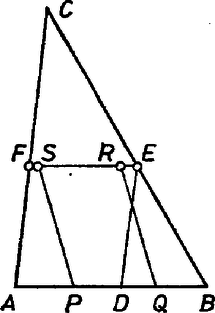 3. ábra Az paralelogramma alapja ugyanis nem kisebb -nál, és ugyanakkora magasság tartozik hozzá, mint -ben -hoz. Az -ről és a hasonló elhelyezkedésű paralelogrammákról fogjuk bebizonyítani, hogy területük legfeljebb fele a háromszög területének. A , , pontok illeszkedjenek rendre az , , oldalra. Ha a oldal felezőpontja, akkor az paralelogramma területe fele az háromszög területének. Ha nem felezi -t, akkor feltehetjük, hogy a csúcshoz közelebb van, mint -hez, mivel az és oldalak szerepe felcserélhető. Legyen az oldalnak az a pontja, amelyre (4. ábra). 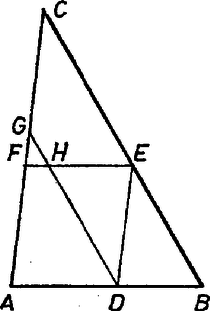 4. ábra Mivel , ezért és metszik egymást. A metszéspontot jelöljük -val. Az és egyenlő területű paralelogrammák által kétszeresen lefedett háromszög területe egyenlő a háromszög területével, hiszen a két háromszög egybevágó. Ebből következik, hogy az háromszög területe éppen az háromszög területével nagyobb, mint az paralelogramma területének kétszerese. Baráti Ákos, (Győr, Czuczor G. Bencés Gimn., I. o. t.) dolgozata alapján |