| Feladat: | Gy.1963 | Korcsoport: 16-17 | Nehézségi fok: könnyű |
| Füzet: | 1981/október, 72. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1981/február: Gy.1963 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A szóban forgó kör (a továbbiakban kör) középpontját jelöljük -mal. A és körök középpontjait jelöljük -gyel, ill. -vel, érintési pontjukat -ve1, a egyenest pedig -vel. 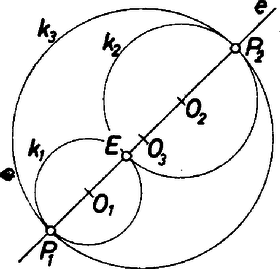 1. ábra 2. Ha úgy metszi a , köröket, hogy nem halad át az , pontokon, akkor , és valódi háromszögek, és egyenlő szárúak (2. ábra). 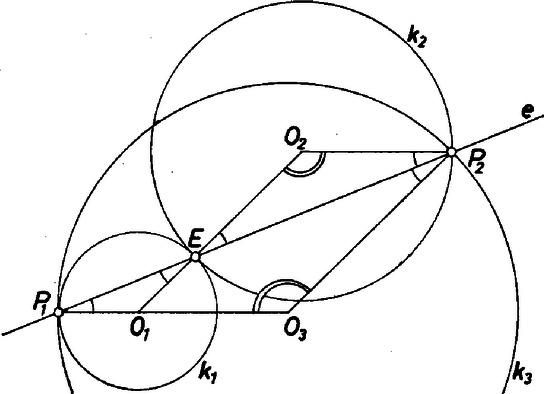 2. ábra Az , szögek csúcsszögek lévén egyenlőek. Így a három egyenlő szárú háromszög alapon fekvő szögei egyenlőek. Az négyszög paralelogramma, mert benne a -nél levő szög mindkét szomszédját -ra egészíti ki. Mivel a paralelogramma szemközti oldalai egyenlők, . Viszont a kör sugara, pedig a kívülről érintkező és körök sugarainak összegével egyenlő, az állítást ezzel igazoltuk. (L. L.) |