| Feladat: | Gy.1957 | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Fodor Gyula | ||
| Füzet: | 1981/november, 142 - 143. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Pont körüli forgatás, Egyéb szinezési problémák, Szabályos sokszögek geometriája, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1981/január: Gy.1957 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tekintsük az öt piros pont által meghatározott ötszöget. A tízszög középpontja körül ezt az ötszöget forgassuk el valamelyik irányba -kal, amíg önmagába vissza nem tér. Ha az így meghatározott ötszögek valamelyikének csúcsai között található három kék, akkor a feladatbeli állítás nyilván teljesül. 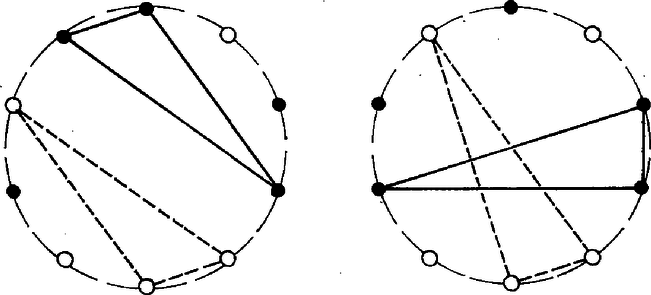 Tegyük fel, hogy egyik ötszögben sincs három kék csúcs. Ekkor a teljes körülforgatás közben összesen legfeljebb kék csúcspont található. A körülforgatás során egy-egy tízszög-csúcson áthaladt mind az öt ötszög-csúcs, ezért minden egyes kék pontot ötször számoltunk. Mivel öt kék pont van, összesen huszonöt pontot kellett volna összeszámolnunk. Itt ellentmondásra jutottunk, tehát a feltételezett eset nem állhat fenn. Ezzel a feladatban szereplő állítást igazoltuk. Fodor Gyula (Bp., Apáczai Csere J. Gyak. Gimn., I. o. t.) Megjegyzések. 1. A feladat állításánál többet bizonyítottunk. Nevezetesen: a talált egybevágó háromszögek nemcsak egybevágók, hanem síkbeli forgatással is átvihetők egymásba. 2. Próbáljuk alkalmazni a megoldásban használt bizonyítási eljárást szabályos szögre. Ennek csúcsát festjük pirosra, -et pedig kékre. esetén biztosan van olyan háromszög, amelyiknek minden csúcsa piros, és amelyikhez található vele egybevágó csupa kék csúcsú háromszög.  Az egyenlőtlenség minden -nál nagyobb egész számra teljesül. Tehát már szabályos nyolcszögre is igaz az állítás. Sőt! Szinte hihetetlen, de ez az állítás szabályos hatszögre is érvényes (lásd az ábrákat!). Persze ekkor már az egybevágó háromszögeket nem mindig tudjuk egymásba síkbeli forgatással átvinni. |