Feladat: Gy.1956 Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1981/november, 141 - 142. oldal  PDF  |  MathML 
Témakör(ök): Térgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):Feladatok: 1981/január: Gy.1956

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a három félegyenest a-val, b-vel, c-vel, és a szóban forgó merőlegeseket rendre a0-lal, b0-lal, c0-lal. Legyen továbbá C0 a c félegyenes tetszőleges, P-től különböző pontja, és S a C0-on átmenő, c-re merőleges sík. Mivel a és b a c-vel hegyesszöget zár be, mindkettő metszi S-t, jelöljük a metszéspontokat A-val, B-v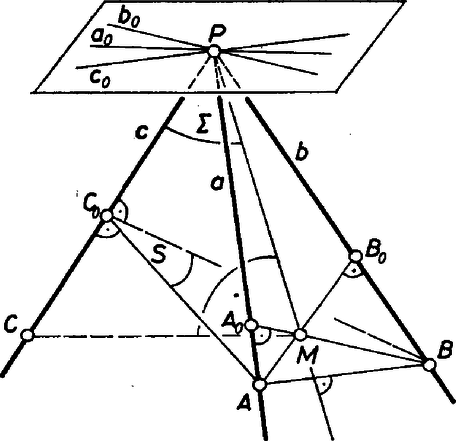el.


A kapott AB egyenes benne van az a és b által meghatározott síkban, és merőleges c-re, hiszen S-ben is benne van. Ezért AB párhuzamos c0-lal. Jelöljük A-nak b-n levő vetületét B0-lal, B-nek a-n levő vetületét pedig A0-lal. Mivel a és b hegyesszöget zárnak be, az AB0 és BA0 egyenesek metszik egymást, és M metszéspontjuk az ABP háromszög magasságpontja. Emiatt a PM egyenes merőleges AB-re, és ha nem azonos c-vel, akkor azzal együtt AB-re merőleges síkot határoz meg. (Mivel PM és c akkor azonosak, ha c benne van az a és b által meghatározott síkban, ettől az esettől eltekinthetünk, hiszen ekkor a feladat állítása nyilvánvaló.) Jelöljük a c és PM egyenesek által meghatározott síkot Σ-val. Abból, hogy Σ merőleges AB-re, következik, hogy Σ merőleges az ABP síkra is, és ha Σ-ban az M ponton át PM-re merőlegest állítunk, az egyben az ABP síkra is merőleges lesz. Mivel c egyenese nem merőleges az ABP síkra és benne van Σ-ban, c egyenese metszi ezt a merőlegest, jelöljük a metszéspontot C-vel, Az a egyenese merőleges a BA0, CM egyenesekre, tehát merőleges BC-re is, és így BC∥a0. Hasonlóan kapjuk, hogy AC∥b0, tehát az a0, b0, c0 egyenesek párhuzamosak az ABC síkkal. Mindhárom egyenes átmegy P-n, ezért a három egyenes valóban egy síkban van, amint azt bizonyítanunk kellett.
 

II. megoldás. Jelöljük a félegyeneseket most is a-val, b-vel, c-vel. A feladat állításának igazolásához elegendő mindegyik félegyenesen egy-egy pontot: A-t, B-t, illetve C-t találni úgy, hogy a⊥BC, b⊥CA és c⊥AB teljesüljön, hiszen ekkor a kérdéses merőlegesek mind benne vannak abban a P-n átmenő síkban, amely párhuzamos az ABC sík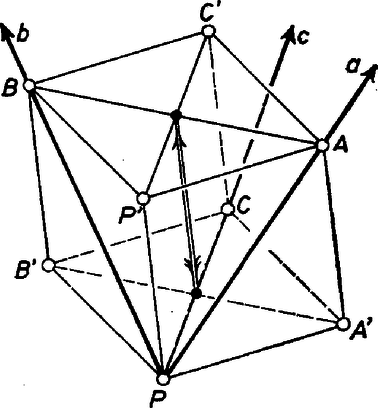kal.

Legyen tehát A az a félegyenes tetszőleges pontja, és állítsunk A-ból merőleges síkot c-re. Ez a sík a félegyenesekre tett kikötéseink alapján metszi a b félegyenest, legyen a metszéspont B. Hasonlóan a B-ben emelt, a-ra merőleges sík metszi a c félegyenest, a metszéspontot C-vel jelöljük.
A most kapott A, B, C pontokra AB⊥c, illetve BC⊥a a pontok megválasztása miatt teljesül, s így csak az van hátra, hogy megmutassuk: CA⊥b. Ehhez toljuk el a PC szakaszt a P'C' helyzetbe úgy, hogy P'C' felezőpontja az AB felezőpontjával essen egybe, s az AB szakaszt az A'B' helyzetbe úgy, hogy ennek felezőpontja a PC szakasz felezőpontjával essen egybe. Az így kapott PA'CB'P'AC'B hatlapú idomot paralelepipedonnak nevezik, lapjai paralelogrammák, szemben álló lapjai párhuzamosak és egybevágók.
Mivel AB⊥c, azért A'B'⊥PC is igaz, tehát a PA'CB' lap (és a vele egybevágó P'AC'B lap is) rombusz. Hasonlóan BC⊥a miatt P'A'⊥PA, és így a PA'AP' és a B'CC'B lap is rombusz. Ebből pedig következik, hogy a paralelepipedon összes éle egyforma hosszú, tehát a harmadik lappár is rombuszokból áll. Így P'B'⊥PB, vagyis AC⊥b, ahogyan azt állítottuk.