| Feladat: | Gy.1951 | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Füzet: | 1981/november, 138 - 139. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikai leszámolási problémák, Sakktáblával kapcsolatos feladatok, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1981/január: Gy.1951 | ||
|
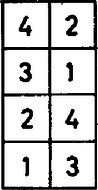
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A sakktáblán a ló fehér mezőről feketére, feketéről pedig fehérre lép. Ez azt jelenti, hogy azonos színű mezőkön álló lovak közül semelyik kettő sem üti egymást. A -as sakktáblán fekete és fehér mező van, így itt ló elhelyezhető a kívánt módon, ha például a fehér mezőkre állítjuk őket. Az -ös sakktáblán az egyik színből , a másikból pedig mező van, ezen a táblán tehát legalább ló helyezhető el.
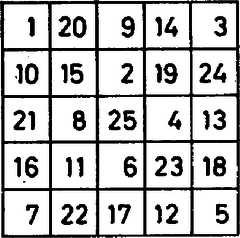
Felállítható-e a táblákra a fentieknél több ló is az adott feltétellel? Tekintsünk egy -es táblarészletet. Az itt található mező számmal megszámozható úgy, hogy az azonos számú mezőkön álló lovak üssék egymást. Egy ilyen számozást mutat az ábra. Így egy ilyen részletre négynél több ló nem kerülhet, hisz különben feltétlenül volnának azonos számú mezőkön álló, tehát egymást ütő lovak. Mivel pedig a -as sakktábla felépíthető darab -es részből, így -nél több ló már nem lehet a táblán. Fenti eredményünk tehát a lehető legjobb. 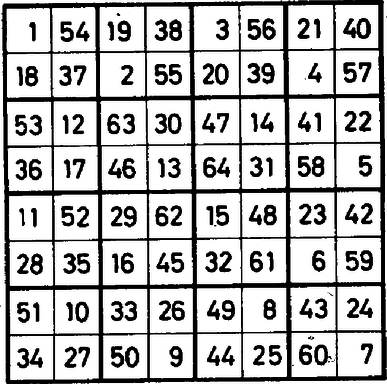 3. ábra Az -ös tábla nem rakható össze -es téglalapokból, így itt más módszerre van szükség. A ábrán -től -ig megszámoztuk az -ös tábla mezőit. Könnyen ellenőrizhető, hogy ha egy ló az számú mezőről kiindulva mindig a soron következő számú mezőre lép, akkor lépésben minden mezőt érint. Így ha -nál több lovat állítunk fel az -ös táblára, akkor ezek közt feltétlenül lesz legalább kettő, amelyek szomszédos sorszámú mezőkre kerülnek, tehát a számozás tulajdonsága miatt ütik egymást. Az -ös táblán tehát ló elhelyezhető a kívánt módon, annál több már nem. Megjegyzés. Az utóbbi módszer a -as tábla esetén is megadja a megfelelő felső határt, ha felhasználjuk azt az ismert tényt, hogy egy -as sakktábla is bejárható lóugrásokkal. Ilyen bejárást adunk meg a ábrán. |