| Feladat: | Gy.1940 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Danyi Pál , Törőcsik Jenő | ||
| Füzet: | 1981/április, 163 - 165. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Permutációk, Szabályos sokszögek geometriája, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1980/november: Gy.1940 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Számozzuk meg a sokszög csúcsait -től -ig tetszőleges csúcson kezdve a számozást, és mondjuk az óramutató járásával megegyező irányban járva be a csúcsokat. Rendeljük a számozás alapján a sokszög tetszőleges két csúcsát összekötő szakaszhoz a végpontokhoz írt számok összegét. Vizsgáljuk meg először, hogy mit kapunk, ha a törtvonalban szereplő szakaszokhoz rendelt számokat összeadjuk. Ebben az összegben -től -ig minden szám kétszer szerepel, hiszen minden csúcsból két szakasz indul ki. Az összeg tehát a csúcsok sorrendjétől függetlenül az első pozitív egész szám összegének a kétszerese. Írjuk le kétszer -től -ig a számokat, de úgy, hogy másodszor fordított sorrendben írjuk őket: Most azt vizsgáljuk meg, hogy mit mondhatunk két szakasz számairól, ha azok párhuzamosak. A szakaszok négy végpontja a kört négy körívre vágja, ezek közül kettő a két párhuzamos közti sávban van, kettő azon kívül. Két esetet különböztetünk meg aszerint, hogy az ív hova kerül. 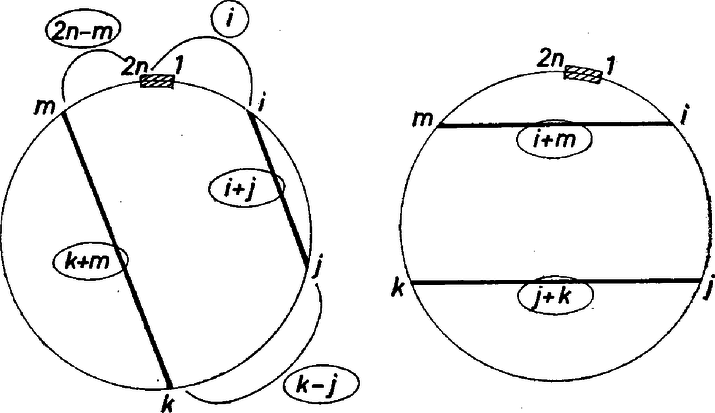 Ha a két párhuzamos között van ez az ív, jelöljük a végpontokhoz írt számokat nagyság szerint növekedve -vel, -vel, -val, -mel. Mivel egy körből párhuzamos egyenesek egyenlő íveket metszenek ki, most
Meg kell még vizsgálni azt az esetet, amikor az ívecske nem esik a párhuzamosok közé. A csúcsokat most is nagyság szerint jelölve a párhuzamosság feltételei , vagyis
Minden esetre érvényes az a megállapítás, hogy a párhuzamos szakaszokhoz rendelt összegek -nel osztva ugyanazt a maradékot adják. Ez az észrevétel a megoldás kulcsa. Először is megmutatjuk, hogy ez az állítás megfordítható. Mivel a számok és közöttiek, az összegek kisebbek -nél. Így csak úgy lehetnek a maradékok egyenlőek, ha az összegek is egyenlőek, vagy ha az összegek különbsége . Az első esetben az egyik végpontjaihoz rendelt számokat -vel, -mel jelölve, a másikét pedig -vel, -val, a (2) összefüggést, majd ebből a párhuzamosságot biztosító feltételt kapjuk. A másodikban pedig előbb (1)-et kapjuk, majd abból a párhuzamosságot, ha és az eredeti két szakasz. Végül megmutatjuk, hogy ellentmondásra vezet az a feltétel, hogy a töröttvonalnak nincsenek párhuzamos darabjai. Ekkor ugyanis a szakaszokhoz rendelt összegek -nel osztva páronként különböző maradékot adnának. Mivel a szakaszok száma is , és a lehetséges maradékok száma is , ez csak úgy lehetne, ha minden maradékot pontosan egyszer kapnánk meg. Ez viszont azt jelentené, hogy a maradékok összege az első pozitív egész szám összegével volna egyenlő, ami az előbb kapott kétszeres összeg fele. Mivel pedig a maradékokhoz úgy jutunk, hogy az összegeket vagy változatlan hagyjuk, vagy -nel csökkentjük, a csökkentések összege -nel osztható. Ámde fele nem osztható -nel, tehát valóban ellentmondásra vezet a mondott feltétel. Danyi Pál (Pécs, Nagy Lajos Gimn., II. o. t.) Megjegyzés. A feladatban szereplő tétel bizonyítása megtalálható Szabó Sándor: Egy szabályos sokszögre vonatkozó észrevétel című dolgozatában (Matematikai Lapok, 28. évf., 1‐3. szám (1980), 199‐201. oldalak). Törőcsik Jenő (Budapest, Fazekas M. Gyak. Gimn., II. o. t.) |