Feladat: Gy.1939 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bogár Á. ,  Csúri Piroska ,  Görög Zita ,  Hetyei Judit ,  Jaklis S. ,  Juhász Cs. ,  Katona Gy. ,  Kocsis Csilla ,  Miszori I. ,  Náray M. ,  Párkányi I. ,  Peták T. ,  Szederkényi Edit ,  Törőcsik J. ,  Végh Katalin ,  Vindics I. ,  Zieger B. 
Füzet: 1981/május, 201 - 203. oldal  PDF  |  MathML 
Témakör(ök): Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Gyakorlat, Mértani középtételek derékszögű háromszögekben
Hivatkozás(ok):Feladatok: 1980/november: Gy.1939

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. M nyilván különbözik A-tól, különben k nem rajzolható meg. Kössük össze B-t M-mel, és legyen A-nak a BM-en levő merőleges vetülete S. Ebből az S-ből az AB szakasz is, az AM szakasz is derékszög alatt látszik, tehát S az AM feletti k, és az AB feletti k1 Thalész-körön is rajta van. Mindkét kör átmegy A-n is, emiatt AS az az egyenes, amelyik P-t metszi ki b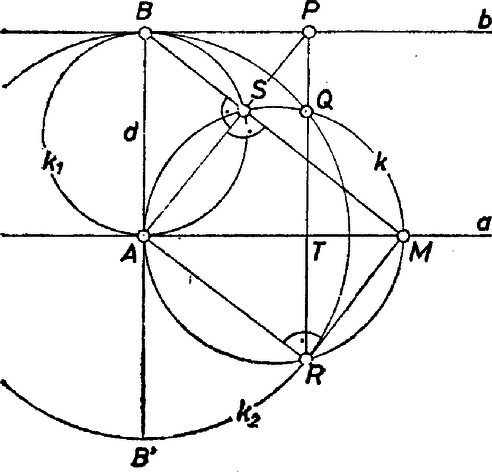-ből.
A közös befogójú ABM, ABP derékszögű háromszögek úgy helyezkednek el, hogy az egyik átfogója a másikban magasságvonal, és mindkettő hasonló az ABS háromszöghöz.


Emiatt a két háromszög megfelelő befogóinak aránya egyenlő
AM:AB=AB:BP.(1)

Mivel M is, P is az AB egyenesnek ugyanazon az oldalán van, mint S, a P-n átmenő, AB-vel párhuzamos egyenes akkor metszi az AM szakaszt, ha BP≦AM, ami (1) miatt azzal ekvivalens, hogy AM≧AB. Nyilván ugyanekkor metszi ez az egyenes k-t is, és
AT⋅AM=AQ2=AR2,(2)
ahol T a P, Q, R pontok a-n levő vetülete. Ha ugyanis T azonos M-mel, akkor Q és R is azonos M-mel, és (2) triviális; különben Q és R az a-ra tükrösen helyezkedik el, és (2) azAMQ, AMR derékszögű háromszögekben az AQ, AR befogónak az átfogóra eső vetületére vonatkozó ismert összefüggés miatt igaz.
Az (1) és (2) összefüggések, valamint AT=BP miatt AQ=AR=AB, vagyis a Q, R pontok az A körüli, B-n átmenő k2 körnek a-ra tükrösen elhelyezkedő pontjai. Mivel M nem lehet azonos A-val, Q, R egyike sem lehet B-vel, sem annak a-ra vonatkozó B' tükörképével azonos. Megmutatjuk, hogy minden más Q, R pontpár előállítható M alkalmas megválasztásával. Legyen ugyanis U a Q, R pontoknak a-n levő közös vetülete, és mérjük fel az AU félegyenesre az AM=AB2/AU szakaszt. Tudjuk már, hogy ebből az M-ből kiindulva k2-nek olyan a-ra szimmetrikus pontpárját kapjuk, amelyek a-n levő T vetületére AT=AB2/AM=AU. Mivel T is, U is az AM szakaszon van, ebből következik, hogy T és U azonosak, tehát M-ből kiindulva éppen az adott Q, R pontpárt kapjuk.
 

II. megoldás. Válasszuk a koordináta-rendszer x tengelyének az a egyenest, origójának az A pontot, és használjuk változtatás nélkül az I. megoldásban bevezetett jelöléseket. A k és k1 körök egyenlete
x2+y2=mx,(3)x2+y2=dy,(4)
ahol m az M abszcisszáját, d pedig a B ordinátáját jelöli. Tudjuk, hogy a két kör metszi egymást, hiszen az origón mindkettő átmegy, de itt nem érintik egymást. A két kör közös  pontjainak ordinátáira (3) is, (4) is teljesül, tehát ezekre a két egyenlet különbségeként kapott
mx=dy(5)
összefüggés is érvényes. Ez mindig egyenes egyenlete, hiszen d≠0. Ez tehát a két kör metszéspontjain átmenő egyenes egyenlete. A P pontnak, mint a b egyenes minden pontjának, az ordinátája d, tehát P abszcisszája d2/m. (Itt m≠0, hiszen M az A-tól különböző pont.) Ugyanennyi a Q, R pontok abszcisszája is, így ezek ordinátája (3) alapján
y=±d2m(m-d2m);

Ebből kiolvasható, hogy a Q, R metszéspontok akkor jönnek létre, ha |m|≧|d| és ha létrejönnek, akkor (3) alapján mindkettő koordinátáira
x2+y2=d2(6)
teljesül, ami az origó körül rajzolt d sugarú kör egyenlete. Tudjuk, hogy a Q, R pontok abszcisszája d2/m alakú, tehát nem lehet 0. Ha különben Q, R a (6) egyenletű kör egyenlő abszcisszájú pontjai, és közös abszcisszájukat q jelöli, akkor az m=d2/q értékből kiindulva ugyancsak q abszcisszájú P pontot kapunk, és azon át visszajutunk a Q, R pontokhoz.
Tehát a Q, R pontok az A középpontú, B-n átmenő kör a-ra szimmetrikus pontjai, Q és R lehetnek azonosak, de a Q,R pár nem lehet a B, B' párral azonos.