Feladat:	Gy.1933	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	1981/március, 117. oldal		PDF  |  MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Hossz, kerület, Gyakorlat, Beírt kör
Hivatkozás(ok):	Feladatok: 1980/október: Gy.1933

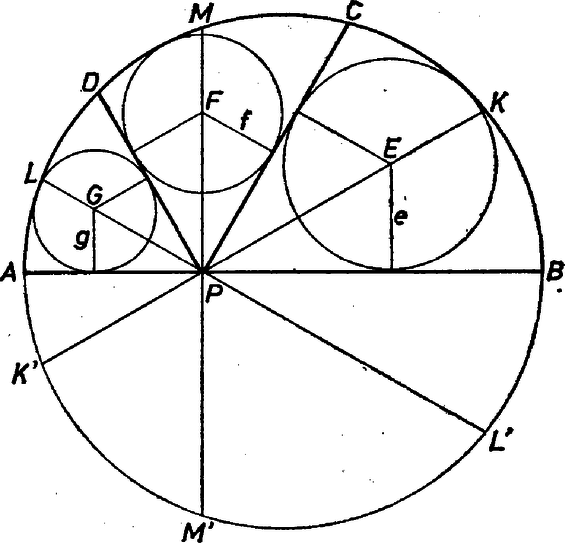
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük a $PBC$, $PCD$, $PDA$ idomokba beírt körök középpontjait rendre $E$-vel, $F$-fel, $G$-vel, sugaraikat $e$-vel, $f$-fel, $g$-vel. Mivel a $PE$, $PF$, $PG$ félegyenesek mind ${60}^{\circ }$-os szögek felezői, $\begin{array}{c}{\displaystyle PE=2e\mathrm{,}PF=2f\mathrm{,}PG=2g\mathrm{.}}\end{array}$ (1) Jelöljük ezeknek a félegyeneseknek az eredeti körrel alkotott metszéspontjait rendre $K$-val, $M$-mel, $L$-lel. Ezek nem lehetnek az egyes idomokba írt körök belső pontjai, így $\begin{array}{c}{\displaystyle EK\ge e\mathrm{,}FM\ge f\mathrm{,}GL\ge g\mathrm{,}}\end{array}$ (2) amit (1)-gyel összevetve kapjuk, hogy $\begin{array}{c}{\displaystyle PK+PM+PL\ge 3\left(e+f+g\right)\mathrm{.}}\end{array}$ Elegendő tehát belátni, hogy $\begin{array}{c}{\displaystyle PK+PM+PL\le 3R\mathrm{.}}\end{array}$ Jelöljük a $PK$, $PM$, $PL$ egyeneseknek az eredeti körrel alkotott második metszéspontjait rendre $K\text{'}$-vel, $M\text{'}$-vel, $L\text{'}$-vel. Akkor $L$ és $K\text{'}$, $M$ és $M\text{'}$, $K$ és $L\text{'}$ az $AB$-re szimmetrikusan helyezkednek el, emiatt $\begin{array}{c}{\displaystyle 2\left(PK+PM+PL\right)=\left(PK+PL\text{'}\right)+\left(PM+PM\text{'}\right)+\left(PL+PK\text{'}\right)\mathrm{.}}\end{array}$ Ez utóbbi összeg viszont nem más, mint a $KK\text{'}$, $MM\text{'}$, $LL\text{'}$ húrok összhossza, ami nyilvánvalóan legfeljebb $6R$. Egyenlő csak akkor lehet vele, ha a húrok mindegyike átmérő, vagyis $P$ az $AB$ szakasz felezőpontja. Mivel ekkor (2)-ben is az egyenlőség érvényes, ebben (és csakis ebben) az esetben $e+f+g=R$, különben $e+f+g<R$, amint azt bizonyítani kellett.