Feladat: Gy.1932 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1981/április, 160. oldal  PDF  |  MathML 
Témakör(ök): Terület, felszín, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1980/október: Gy.1932

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az AC átlón először felvett pontot Q-val, és húzzunk P-n át is a paralelogramma oldalaival párhuzamos egyeneseket. Az AB-vel párhuzamos, P-n, illetve Q-n átmenő egyenesek az AD, BC egyenesekkel együtt egy paralelogrammát fognak közre,jelöljük ennek a területét tAB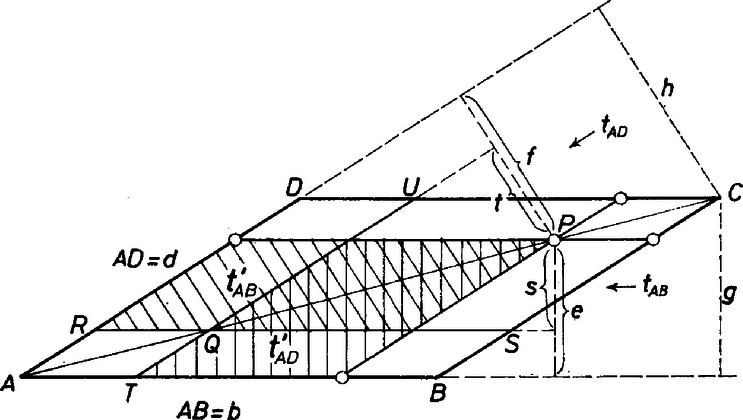-vel.


Ha mondjuk RS, TU közül RS párhuzamos AB-vel, akkor tAB a PRS háromszög területének a kétszerese, hiszen egyenlő RS hosszának és P-nek az RS-től mért távolságának a szorzatával. Legyen még tAD a P-n, Q-n átmenő, AD-vel párhuzamos egyenesek, és az AB, CD egyenesek által közrefogott paralelogramma területe. RS‖AB esetén tAD a PTU háromszög területének a kétszeresével egyenlő. Így elegendő belátni, hogy tAB és tAD egyenlőek.
Mivel most már P és Q szerepe megegyezik, feltehetjük, hogy közülük mondjuk Q van A-hoz közelebb. Tekintsük először azt a paralelogrammát, amelynek A és P csúcsa, és oldalai rendre párhuzamosak (vagy azonosak) az eredeti paralelogramma megfelelő oldalaival. Jelöljük a vizsgált sávok ebbe eső darabjainak a területét t'AB-vel, illetve t'AD-vel, ezek egyenlősége ismeretes. Ugyancsak tudjuk azt is, hogy a sávoknak a QC átlójú paralelogrammába eső darabjainak t''AB, t''AD területe egyenlő. Mivel a (t'AB+t''AB) összeg ugyanannak a PQ átlójú paralelogrammának a területével haladja meg tAB-t, mint amivel (t'AD+t''AD) a tAD értékét meghaladja, ezekből már következik tAB és tAD egyenlősége.
 
II. megoldás. Legyen továbbra is RS, TU közül RS párhuzamos AB-vel, és jelöljük az AB, AD szakaszok hosszát b-vel, d-vel, a PRS, PTU háromszögek P-hez tartozó magasságát s-sel, t-vel. Azt kell belátnunk, hogy bs=dt, vagyis s:t=d:b. Jelöljük P-nek az AB, AD egyenesektől mért távolságát e-vel, f-fel. A párhuzamos szelők tétele szerint e:s=AP:PQ (ahol Q most is RS és TU metszéspontját jelöli), és f:t=AP:AQ, tehát e:s=f:t, vagyis s:t=e:f. Jelöljük végül C-nek az AB, AD egyenesektől mért távolságát g-vel, h-val. Ismét a párhuzamos szelők tétele alapján e:g=AP:AC, f:h=AP:AC, tehát e:f=g:h.
Ezek szerint azt kell belátni, hogy g:h=d:b, vagyis bg=dh. Ez viszont nyilvánvaló, hiszen mindkettő az ABCD paralelogramma területével egyenlő.