Kezdőlap


Feladat:	Gy.1923	Korcsoport: 14-15	Nehézségi fok: nehéz
Füzet:	1981/január, 20 - 21. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Gyakorlat, Háromszögek egybevágósága
Hivatkozás(ok):	Feladatok: 1980/szeptember: Gy.1923

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Három részre vágjuk a kérdezett mértani helyet aszerint, hogy a háromszögek közül melyek egybevágóak.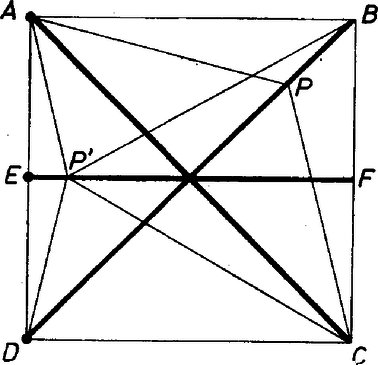
Ha a $P A B$ , $P B C$ háromszögek egybevágóak, területük is egyenlő. Mivel bennük $A B = B C$ , a megfelelő magasságok is egyenlőek. Ez azt jelenti, hogy $P$ az $A B$ , $B C$ egyenesektől egyenlő távolságra van, vagyis rajta van a két egyenes egyik szögfelezőjén. Mivel $P$ a négyzet belső pontja, a $B D$ szakaszon kell lennie. Ennek bármely belső pontja meg is felel, mert ha $P$ a $B D$ szakaszon van, a $P A B$ háromszög $B D$ egyenesre vonatkozó tükörképe a $P C B$ háromszög.

Ha a

P B C, P C D

háromszögek egybevágóak, az előbbi meggondolásban

A B

helyett mindenütt

C D

-t mondva kapjuk, hogy a mértani hely az

A C

szakasz belseje.
Ha a

P A B

P C D

háromszögek egybevágóak,

A B = C D

miatt most

P

-nek az

A B

C D

egyenesektől kell egyenlő távolságra lennie, vagyis rajta kell lennie a négyzet

E F

középvonalán, ahol

E

A D

F

B C

szakasz felezőpontja. Az

E F

szakasz minden belső pontja meg is felel, hiszen a

P A B

háromszögnek az

E F

egyenesre vonatkozó tükörképe épp a

P D C

háromszög.
A kérdezett mértani hely tehát az

A C

B D

E F

szakaszok belsejének együttese.

Megjegyzés. A négyzet határán az

A, D, E, F

pontok tartoznának a mértani helyhez, a négyzeten kívül a mondott szakaszok meghosszabbításai. Igen sok dolgozat hiányos, mert a mértani hely kettős tulajdonsága közül valamelyik bizonyítása hiányzik belőlük. Akik a mértani helyet rosszul adták meg (elhagytak belőle vagy hozzátettek valamit), azoknak a dolgozatát hibásnak minősítettük. (K. T.)