Kezdőlap


Feladat:	Gy.1914	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1981/február, 69 - 70. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat, Síkgeometriai bizonyítások, Alakzatok hasonlósága
Hivatkozás(ok):	Feladatok: 1980/május: Gy.1914

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $B$ ponton keresztül húzzunk párhuzamost az $A D$ egyenessel, messe ez a $D C$ -t $F$ -ben. Majd húzzunk egy $A B$ -vel párhuzamost a $D$ pontton keresztül, messe ez $B C$ -t az $E$ -ben. Belátjuk, hogy az $A B C D$ és $M F C E$ négyszögek hasonlóak, a csúcsokat a felsorolás sorrendjében feleltetve meg egymásnak.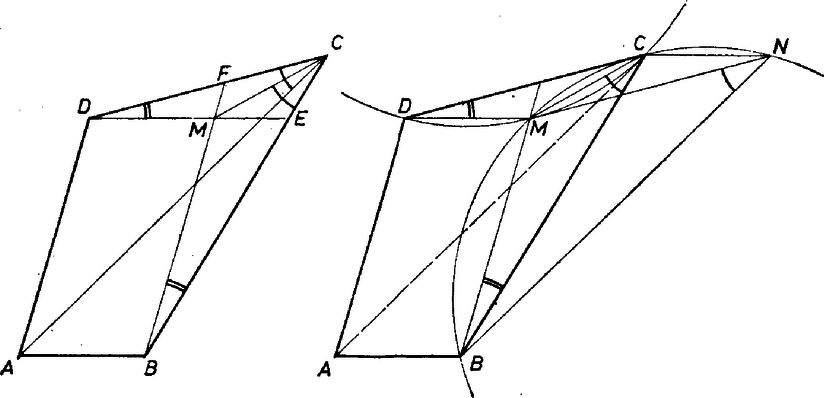

D M F

és

B M E

háromszögekben az

F D M

és

M B E

szögek a feltétel szerint egyenlők. Az

F M D

és

E M B

szögek viszont csúcsszögek, amiből következik, hogy a két háromszög hasonló, így megfelelő oldalaikra

\frac{F M}{M E} = \frac{M D}{M B} = \frac{A B}{A D}

Vagyis a két négyszög egy‐egy megfelelő oldalpárjának aránya megegyezik. Mivel

D A B ∢ = F M E ∢

, hiszen az

A B M D

idom paralelogramma, valamint a két négyszögben a

C

csúcsnál levő szög közös, így egyenlő, végül

C D A ∢ =

= A B C ∢ = D E C ∢

, a két négyszög valóban hasonló. A hasonlóság miatt pedig az

A C D

és

B C M

szögek egyenlősége is fennáll.

II. megoldás. Tekintsük a

C M B

C M D

háromszögek köré írható köröket. Ezekben a

C M

húr közös, és hozzá egyenlő látószögek tartoznak. Emiatt a két kör sugara egyenlő, ha például a másodikat a

C M

szakasz felezőpontjára tükrözzük, az elsőt kapjuk. (Mivel

M

A B C D

négyszögben belső pont, a két kör a

C M

egyenes ellentétes partjain fekszik.) E tükrözés a

D M

szakaszt a vele párhuzamos és egyirányú

C N

szakaszba viszi. Tehát a

B M

szakasz a

C

N

pontokból egyenlő szögek alatt látszik. Ezzel viszont igazoltuk a feladat állítását, hiszen a

B M N

háromszöget

C N

mentén eltolva az

A D C

háromszöget kapjuk.

Megjegyzés. A feladat az 1980. évi Arany Dániel matematikai tanulóverseny II. fordulóján a haladó (II. osztályos) általános tantervű osztályok versenyének első feladata volt.