Kezdőlap


Feladat:	Gy.1899	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1980/december, 215 - 216. oldal		PDF \| MathML
Témakör(ök):	Eltolás, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1980/március: Gy.1899

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Helyezzük rá a háromszögre a körlapot úgy, hogy $A$ és $B$ , illetve $B$ és $C$ a peremén legyen és a körlap a harmadik pontot is lefedje. Így kapjuk a $k_{1}$ , ill. $k_{2}$ kört. Középpontjukat jelöljük $O_{1}$ és $O_{2}$ -vel. Mivel a körlap sugara nagyobb, mint a háromszög köré írt kör sugara, a $k_{1}$ és $k_{2}$ kör biztosan metszi egymást egy $B$ -től különböző $P$ pontba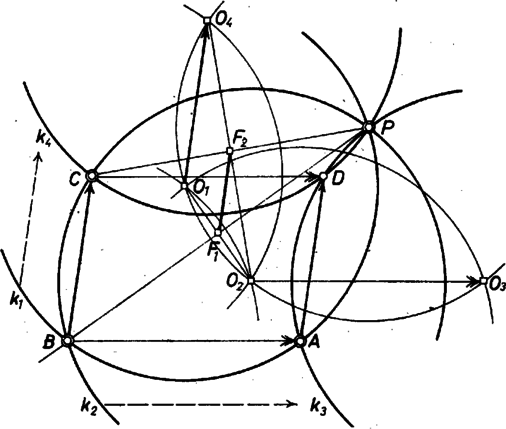n.

Most helyezzük el a körlemezt úgy, hogy

P, A

a kerületére kerüljön és rajzoljuk meg a

k_{1}

től különböző

k_{3}

kört. Majd hasonlóan a

P, C

pontokon átmenő,

k_{2}

-től különböző

k_{4}

kört. Azt állítjuk, hogy ez utóbbi két körnek

P

-től különböző metszéspontja,

D

lesz a paralelogramma negyedik csúcsa, vagy a két kör érinti egymást, és ekkor már

P

paralelogrammává egészíti ki az

A, B, C

pontokat.
Ennek igazolására először azt látjuk be, hogy a

k_{1}

kört

\vec{B C}

vektorral eltolva a

k_{4}

körbe megy át. Mivel a két kör sugara egyenlő, elegendő azt belátnunk, hogy a

\vec{B C}

eltolás

O_{1}

-et

O_{4}

-be viszi át. Tudjuk, hogy a

k_{1}

és

k_{2}

körök metszéspontjain átmenő

B P

egyenes a két kör szimmetriatengelye és merőlegesen felezi a körök középpontját összekötő

O_{1} O_{2}

szakaszt. Jelöljük ezt a felezési pontot

F_{1}

-gyel. Hasonlóképpen az

O_{2} O_{4}

szakasz és az azt merőlegesen felező

C P

egyenes metszéspontját

F_{2}

-vel. Ekkor

F_{1} F_{2}

P B C

és

O_{2} O_{1} O_{4}

háromszögek közös középvonala, ezért

F_{1} F_{2} ∥ B C

F_{1} F_{2} ∥ O_{1} O_{4}

és

F_{1} F_{2}

mindkét oldal felével egyenlő, azaz

B C # O_{1} O_{4}

. Ezzel állításunkat igazoltuk.
Hasonlóképpen láthatjuk be, hogy a

k_{2}

kört

\vec{B A}

-ral eltolva a

k_{3}

-ba megy át, amiből következik, hogy az

A B C D

paralelogramma

D

csúcsa a

k_{3}, k_{4}

körök metszéspontja. Ha

A B C P

eleve paralelogramma, akkor ‐ mint az könnyen látható‐,

k_{4}

-et a

P

-re való tükrözés

k_{3}

-ba viszi, tehát a két kör

P

-ben érinti egymást.