Kezdőlap


Feladat:	Gy.1892	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1980/november, 142 - 143. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Helyvektorok, Gyakorlat, Magasságpont, Körülírt kör
Hivatkozás(ok):	Feladatok: 1980/február: Gy.1892

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $C A$ , $A B$ szakaszok felezőpontját $G$ -vel és $H$ -val, az $A G H$ háromszög magasságpontját $P$ -vel. Ismeretes, hogy a háromszögek középvonalai párhuzamosak a háromszög oldalaival, ezért az $A B C$ , $A H G$ háromszög $A$ -ból induló magasságvonala azonos. Mivel a $B M$ , $H P$ egyenesek egyaránt merőlegesek $A C$ -re, párhuzamosak egymással. Emiatt a $P H$ egyenes középvonal az $A M B$ háromszögben, és $P$ felezi az $A M$ szakaszt. Az $A H F G$ négyszög paralelogramma, melyet a $G H$ átló két egybevágú részre vág, és e részek a $G H$ felezőpontjára nézve szimmetrikusak. Ez a szimmetria $P$ -t $O$ -ba viszi, hiszen 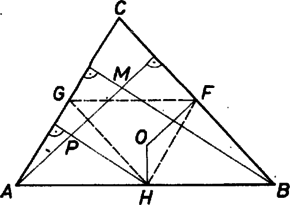$A P ∥ O F$ , $P G ∥ O H$ , $P H ∥ O G$ . Tehát $O F = P A = \frac{1}{2} A M$ .

II. megoldás. Jelöljük általában a

P

-ből

Q

-ba mutató vektort

\vec{P Q}

-val. Megmutatjuk, hogy az

\vec{A M}

2 \cdot \vec{O F}

vektoroknak nemcsak a hosszuk egyenlő, hanem maguk a vektorok is egyenlőek. Ha még az

O

-ból

A

-ba,

B

-be,

C

-be mutató vektorokat rendre a-val, b-vel, c-vel jelöljük, és felhasználjuk, hogy

2 \cdot \vec{O F} = b + c

kapjuk, hogy állításunk ekvivalens az

\begin{matrix} a - \vec{O M} = b + c \end{matrix}

összefüggéssel. Azt kell tehát belátnunk, hogy

\begin{matrix} \vec{O M} = a + b + c . \end{matrix}

(1)

Legyen

M

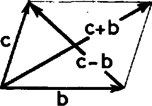az (1) összefüggéssel definiált pont, megmutatjuk, hogy

\vec{A M} ⊥ \vec{B C}

. Valóban,

\vec{B C} = c - b

\vec{A M} = c + b

és a b, c vektorok hossza egyenlő (hiszen

O

A B C

háromszögbe írt kör középpontja). Emiatt a b és c vektorok összeadásához használt paralelogramma rombusz és a

(c + b)

(c - b)

vektorok állását ennek a rombusznak az átlói adják. Hasonlóan látható be, hogy

\vec{B M} ⊥ \vec{C A}

\vec{C M} ⊥ \vec{A B}

Megjegyzés. Hamarabb célhoz érünk, ha az

A B C

F G H

háromszögek hasonlóságára hivatkozunk. Hogy ezt nem tettük, az annak érdekében történt, hogy megmutassuk, esetünkben csak a 2:1 arányú hasonlóság tulajdonságaira van szükség, és ezek még visszavezethetőek az egybevágóság tulajdonságaira. A bizonyított állítás alapján könnyen belátható, hogy az

O M

szakaszt az

A B C

háromszög súlypontja harmadolja. Tovább menve megkaphatjuk az ún. Feuerbach kör tulajdonságait.