Feladat: Gy.1887 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Alberti G. ,  Balázs T. ,  Balázs Z. ,  Benkő Erzsébet ,  Bíró Magdolna ,  Böröczky K. ,  Csesznák A. ,  Csúri Piroska ,  Csörgő T. ,  Danyi P. ,  Fáy J. ,  Fekete Zs. ,  Fonyó L. ,  Fóris Z. ,  Forster E. ,  Guba B. ,  Hemrik F. ,  Horváth 290 P. ,  Ittzés A. ,  Károlyi Gyula ,  Kató G. ,  Kertész Zsuzsa ,  Kő Andrea ,  Kocsis 164 Csilla ,  Kollár P. ,  Kovács 444 G. ,  László G. ,  Markó T. ,  Mikó Teréz ,  Mohay T. ,  Nacsa J. ,  Nagy 513 P. ,  Nyikes P. ,  Parajdi I. ,  Párkány I. ,  Peták T. ,  Regős Enikő ,  Scharle A. ,  Schlarb B. ,  Szabó 354 Zsuzsanna ,  Szabó 509 Z. ,  Szabó E. ,  Szöllősi Z. ,  Tóth 360 G. ,  Tranta Beáta ,  Törőcsik J. ,  Ván 567 P. 
Füzet: 1980/szeptember, 16 - 17. oldal  PDF  |  MathML 
Témakör(ök): Gráfelmélet, Gyakorlat
Hivatkozás(ok):Feladatok: 1980/február: Gy.1887

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítás nyilván teljesül, ha a társaságból mindenki ismer legalább négy embert.
Ha van olyan, aki legfeljebb három embert ismer, akkor ő a társaság további legalább öt tagját nem ismeri. Ezek viszont mind ismerik egymást ‐ mert különben hozzávéve az előző tagot, olyan hármast alkotnának, amelynek tagjai közül senki sem ismeri a másikat ‐ , így mindegyiküknek van legalább négy ismerőse.
Tehát mindig található legalább öt olyan ember, akik közül mindenki legalább négy embert ismer a társaságból.

 

Megjegyzések. 1. A bizonyítás utolsó három mondatában négy helyett n-t, öt helyett (n+1)-et írva a következő általánosított állítás bizonyítását kapjuk: ,,Ha egy 2n+1 tagú társaságból bármely három ember közül legalább kettő ismeri egymást, akkor van legalább n+ 1 olyan tagja a társaságnak, aki legalább n embert ismer a társaságból.''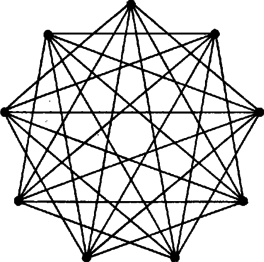
 
 
1. ábra
 

2. Az állítás a következő erősebb formában nem igaz: ,,Van legalább öt olyan ember, akik ismerik egymást.'' Például ‐ pontokkal ábrázolva a társaság tagjait és összekötő szakaszokkal az ismeretségeket ‐ az 1. ábrán olyan társaságot ábrázoltunk, amely a feltételeknek megfelel, és még sincs öt olyan tagja, akik kölcsönösen ismerik egymást. (A feltételnek megfelel, mert tetszőleges három között van olyan kettő, aki nem szomszédos pár, tehát ismeri egymást. Nincs közte öt, aki kölcsönösen ismeri egymást, mert tetszőleges ötből legalább kettő szomszédos, tehát nem ismeri egymást.)
3. Az adott feltételekkel viszont mindig található olyan négy, akik kölcsönösen ismerik egymást. Épp ezt az állítást mondja ki az F. 2201. példa (KöMaL 1979/8-9., 130. o.), de levezethető a következő állítás egyszerű következményeként is: ,,Minden kilenctagú társaságban van négy olyan, akik közül bármelyik kettő ismeri egymást, vagy van három, akik közül senki sem ismeri a másikat.'' (Megtalálható például Andrásfai Béla: Ismerkedés a gráfelmélettel (Tankönyvkiadó, 1971) című könyv 133. oldalán.)
4. Nem igaz, hogy a feltételek mellett mindig van 6 olyan tagja a társaságnak, aki legalább 4 embert ismer. Ilyen esetet mutat a 2. ábra. (Bármely három ember közül legalább kettő egy csoportba tartozik, tehát ismerősök, de csak ötnek van legalább négy ismerőse.)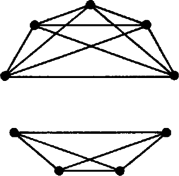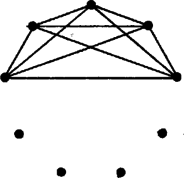
 
 
2. ábra
 

 
3. ábra
 

5. Ha nem teljesül bármely három emberre, hogy van közöttük két egymást ismerő, akkor még teljesülhet, hogy van öt, aki legalább négyet ismer, vagyis az állítás megfordítása nem igaz (3. ábra).
6. A feladat állításából közvetve adódik, hogy ha bármely három emberből legalább kettő ismeri egymást, akkor nem lehet, hogy bármely három ember közül csak egy pár ismeri egymást. Felvethetjük a kérdést: legalább hány ismeretség van a társaságban, ha bármely három emberből kettő ismeri egymást?
A válasz: 16; általában, n tagú társaság esetén pedig: n(n-2)2-[n24]. (Ez Turán Pál egy tételének speciális esete, lásd uo., 148. oldal.) A 2. ábra egy ilyen esetet mutat n=9 esetén.
7. Több megoldó kísérletezett a következő típusú meggondolással: ,,Belátom, hogy a feltétel a társaságban olyan sok ismeretséget biztosít, hogy ez kizárja annak lehetőségét, hogy legfeljebb négy ember ismerjen háromnál több embert.'' Azonban ez a megfontolás esetünkben nem vezethet célra, Ugyanis ehhez annak kellene teljesülnie, hogy 1/2(4⋅8+5⋅3)>23 ismeretségnél is több legyen a társaságban, márpedig ez ‐ mint a 2. ábrán láttuk ‐ nem teljesül feltétlenül.