Kezdőlap


Feladat:	Gy.1884	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Böröczky Károly
Füzet:	1980/október, 69 - 70. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1980/január: Gy.1884

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük fel, hogy találtunk a feltételt kielégítő pontot. Tekintsük az $A P B$ és $A P C$ háromszögek köré írt köröket. Mivel $A P$ a két körnek közös húrja és két ponton keresztül egy meghatározott sugárral, általában két kört tudunk rajzolni, melyek a közös húrra tükrösek, így két eset lehetséges.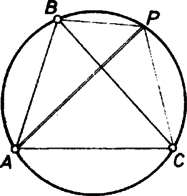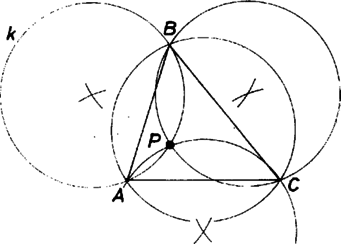
Az első eset, amikor az $A P B$ köré rajzolt kör tartalmazza a $C$ pontot. Ekkor a 3 háromszög köré írt kör egybeesik, és megegyezik az ABC háromszög körülírt körével. Így a $P$ pontok mértani helye a körülírt kör pontjai, kivéve a csúcsokat, mikor nem jön létre az $A P B$ , $B P C$ , $A P C$ háromszög. És fordítva: a kör minden megengedett pontja eleget tesz a feltételnek, hiszen ekkor a körök megegyeznek, s így nyilván sugaruk is egyenlő.

A második eset, ha

C

nincs rajta az

A P B

háromszög köré írt

k

körön, akkor csak az oldalakra vonatkozó tükörképein lehet.

k

-t a háromszög oldalaira tükrözve a tükörkörök mindegyike átmegy a

C

ponton.

C

tehát a tükörkörök

P

-től különböző metszéspontja, és ezért az

A P B

háromszög magasságpontja. Tudjuk ugyanis, hogy a háromszög magasságpontjának az oldalakra vonatkozó tükörképei rajta vannak a háromszög körülírt körén. Így

C P ⊥ A B

A P ⊥ B C

és

B P ⊥ A C

, azaz

P

A B C

háromszög magasságpontja.
A keresett mértani hely tehát az

A B C

háromszög körülírt körének pontjai a csúcsokat kivéve, és a háromszög magasságpontja.

Böröczky Károly (Budapest, Ságvári E. Gyak. Gimn., II. o. t.)