Kezdőlap


Feladat:	Gy.1877	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1980/május, 212. oldal		PDF \| MathML
Témakör(ök):	Négyszög alapú egyéb hasábok, Szögfüggvények a térben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/december: Gy.1877

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az alaplap szóban forgó szárának végpontjait $B$ -vel, $C$ -vel ( $B$ a hegyesszögű csúcs), a fedőlap átellenes szárának hegyesszögű végpontját $E$ -vel, az alaplap $E$ alatti csúcsát $A$ -val, $A$ -nak $B C$ -n levő merőleges vetületét $T$ -vel. Mivel a $B C$ egyenesre $A T$ is és $A E$ is merőleges, $B C$ merőleges az $A E T$ síkra. Emiatt az $A T, E T$ egyenesek szöge egyenlő az $A B C, E B C$ síkok szögével, és az $A E T$ háromszögben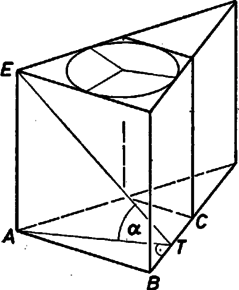

\begin{matrix} A E = A T \cdot tg α . \end{matrix}

Az itt fellépő

A T

szakasz az alaplap

A

csúcsának a

B C

egyenestől mért távolsága. Jelöljük az alaplapba írt kör középpontját

O

-val,

O

-nak

B C

-n levő vetületét

U

-val,

A B

felezőpontját

F

-fel. Ez utóbbinak

B C

-től mért távolsága

A T

felével egyenlő. Ezt megkapjuk, ha

F

-et a

B C

-re merőleges

O U

egyenesre vetítjük: ha a vetület

V

, akkor

U V

a keresett távolság, és

A T = 2 U V

. Az

F O V

háromszögben

O F ⊥ F B, O V ⊥ B U

, így

F O V ∢ = α

és

O V = r cos α

. Ezek alapján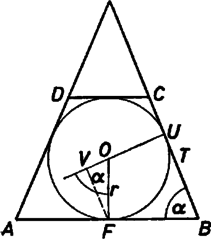

\begin{matrix} A E = 2 U V tg α = 2 (O V + O U) tg α = 2 (r cos α + r) tg α = 2 r (sin α + tg α) . \end{matrix}

Megjegyzés. Megoldásunkban az egyenlő szárú trapézt tengely-szimmetrikusnak vettük, benne a hegyesszögek ugyanazon a párhuzamos oldalon voltak. Ha az elnevezést úgy értelmezzük, hogy négyszögünk egyrészt trapéz, másrészt a szárai egyenlőek, mondhatjuk, hogy a négyszög rombusz is lehetne. Ez kissé erőltetett értelmezés, hiszen a rombusznak nincsenek ,,szárai'', mindenesetre így értelmezve a feladat szövegét, eredményül

2 r tg α

-t kapunk.