Feladat: Gy.1876 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1980/április, 166 - 167. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat, Háromszögek geometriája
Hivatkozás(ok):Feladatok: 1979/december: Gy.1876

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

PAQ és PBQ közös átfogójú derékszögű háromszögek, hiszen QA⊥BC és AP∥BC miatt QA az AP egyenesre is merőleges. Hasonlóan láthatjuk be, hogy BQ⊥BP. QB és PA a PQ szakasz fölé írt Thalész‐körnek húrjai, s ezért felező merőlegeseik a kör középpontjában metszik egymást. R tehát a felező merőlegesek metszéspontja s egyben a Thalész‐kör középpontja, így rajta van a PQ átmérőn. Ezzel a mondott állítást igazoltuk.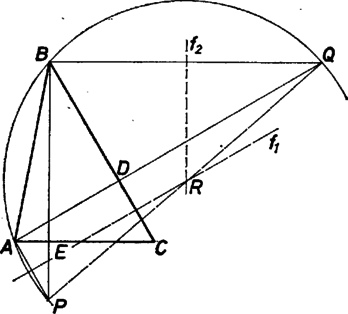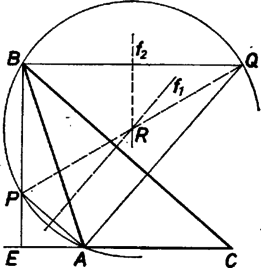

 
 

 
 

A PQ egyenes az A, B pontokat nem választja szét, ha a háromszögnek az A csúcsnál levő szöge hegyesszög. Ha az A szög tompaszög, a B csúcsból húzott magasságvonala a BA egyenesnek a háromszöget nem tartalmazó oldalára kerül, s így a P pont is. Az AD egyenes viszont a háromszög belsejében halad, és mivel QAB∢<CAB∢ és BQ∥CA, a QAB∢+ABQ∢<180∘, azaz AQ és BQ egyenesek az AB egyenesnek P-t nem tartalmazó oldalán metszik egymást. Mindkét esetben az AQB kerületi szög az AB húr ugyanazon ívéhez tartozik, mint az ARB középponti szög. Ha tehát ARB∢=90∘, akkor AQB∢=45∘. De AQB∢=CAD∢ ‐ hiszen váltószögek. A CAD derékszögű háromszögben az egyik hegyesszög 45∘-os, ezért a másik is, azaz a háromszög C csúcsánál levő szöge 45∘-os. Az ARB szög akkor is lehet derékszög, ha a háromszög C csúcsánál levő szög tompaszög. Most is teljesül az AQB∢=12ARB∢=45∘, és az AQB és CAD szögek egyenlősége is, hiszen most egyállású szögek. S mivel CAD∢ a háromszög külső szöge, ezért a háromszög C csúcsánál lévő szöge most 13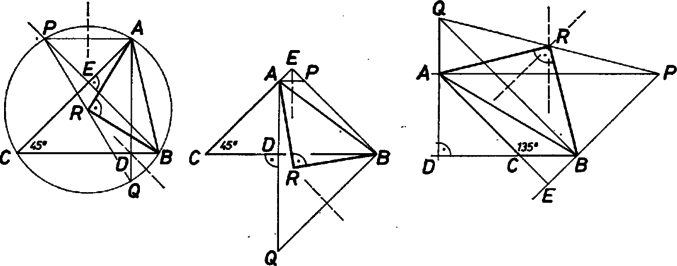5∘-os.