Feladat: Gy.1869 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1980/május, 209 - 211. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1979/november: Gy.1869

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel az A,B,C pontok közül egyiknek sincs kitüntetett szerepe, feltehetjük, hogy B az A és C között van. Az állítást 2 esetben kell külön megvizsgálni: I. ha az M pontnak az A,B,C pontokat tartalmazó e egyenesre való vetülete a pontokat nem választja szét, II. ha M vetülete szétválasztja a pontokat, pl. ha A és B közé esik. Bármely más esetet az A,B,C pontok átbetűzésével megkaphatunk.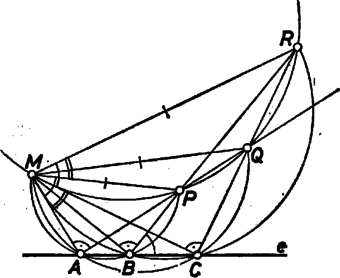
Mindkét esetben igaz az, hogy AMPB,BMCR,AMCQ pontok egy-egy körön, rendre az MP,MR és MQ szakaszok fölé írt Thalész körön vannak, hiszen MAP∢,MBP∢,MCR∢,MBR∢,MAQ∢ és MCQ∢ mindegyike derékszög. A bizonyításban ezeket rendre felhasználjuk.
Ezután nézzük a bizonyítást párhuzamosan a két esetre.

 
 

I. Az AMPB négyszögben az A és B az MP átmérő ugyanazon oldalára esik, AMP∢=PBC∢=RBC∢=RMC∢, a BMCR négyszögből.
Az AMP∢-ből és a vele egyenlő RMC∢-ből vonjuk le a CMP∢-t, ami mindkettőnek része, kapjuk, hogy a különségük is egyenlő
RMC∢-PMC∢=RMP∢,
ill.
AMP∢-PMC∢=AMC∢,
azaz
RMP∢=AMC∢.
Végül az AMCQ négyszögből
AMC∢=AQC∢=PQC∢.
PQC∢-t a PQR∢180∘-ra egészíti ki, de akkor PQC∢=PMR∢ miatt PMR∢+PQR∢=180∘, ami éppen azt jelenti, hogy a PQRM négyszög húrnégyszög.
 
 
II. Most PM az A és B pontokat szétválasztja, így
AMP∢=ABP∢.
Egyrészt
RBC∢=ABP∢=AMP∢,
másrészt a BMCR négyszögből
RBC∢=RMC∢,
és mindkettőhöz PMC-t adva
AMP∢+PMC∢=AMC∢,
RMC∢+PMC∢=RMP∢,
s mivel az összeadandók egyenlők, ezért az összegük is egyenlő, azaz
RMP∢=AMC∢.
Továbbá
PMR∢=AMC∢=180∘-AQC∢=180∘-PQC∢,
amiből
PMR∢+PQR∢=180∘,
mint előbb.
 

Speciális esetként tárgyalhatjuk azokat az eseteket, amikor M vetülete egybeesik valamelyik ponttal.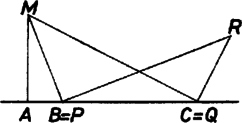
 
 
 

Ha M'=A, akkor nyilván B=P és C=Q. Az MBR∢=MCR∢=90∘ miatt P és Q rajta van az MR szakasz Thalész körén, azaz négyszögünk húrnégyszög. Ha M vetülete B-vel esik egybe, akkor A=P és C=R miatt P,M,Q,R ugyancsak egy körön vannak.