| Feladat: | Gy.1867 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1980/március, 120 - 121. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Numerikus és grafikus módszerek, Terület, felszín, Gyakorlat, Konvex sokszögek | ||
| Hivatkozás(ok): | Feladatok: 1979/november: Gy.1867 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Húzzunk az eredeti ötszög csúcsain át a bennük találkozó oldalakra merőleges, az ötszögből kifelé induló félegyeneseket. Tekintsük minden egyes csúcsban azokat a szögeket, amelyeket úgy kapunk, hogy az ott levő teljes szögből elhagyjuk az ötszögnek az illető csúcshoz tartozó szögét, továbbá az ehhez csatlakozó két derékszöget, amelyek szárait épp az előbb rajzoltuk meg. Így a -os teljes szögből -nál többet, de -nál kevesebbet hagytunk el, tehát mindig marad vissza szög, és az kisebb -nál. A visszamaradó szögek összege , hiszen az ötszöget körbe járva az előbb megrajzolt félegyenesek iránya pontosan egy körforgást végez. 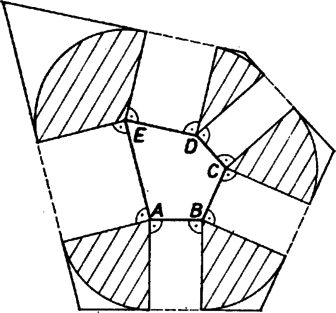 Mérjünk fel a visszamaradó szögek száraira a csúcsukból indulva egységnyi szakaszokat, és ezek végpontjában emeljünk a szárakra merőlegeseket. Mivel a szárakból és a most megrajzolt merőlegesekből álló alakzat szimmetrikus a szögeket felező egyenesekre, új merőlegeseink a szögfelezőkön metszik egymást. Ezeket a merőlegeseket különben úgy is megkaphattuk volna, hogy az eredeti oldalakat önmagukkal párhuzamosan egységgel kifelé toljuk. Ilyenkor tehát az eredeti ötszöghöz öt téglalap és öt deltoid csatlakozik. Rajzoljuk meg a csúcsok körüli egység sugarú köröknek a deltoidokba eső cikkeit. Az ötszög területe többel nőtt, mint e cikkek együttes területe. Mivel a cikkekből pontosan egy teljes kört állíthatunk össze, területük összege . A feladat állítását ezzel bebizonyítottuk. Megjegyzés. Az állítás (és a fenti bizonyítás) ötszög helyett tetszőleges konvex sokszögre érvényes. |