Feladat: Gy.1866 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Alberti G. ,  Balogh 151 Zs. ,  Bánhegyi B. ,  Bocsák A. ,  Bocsák B. ,  Bozsó P. ,  Bukor J. ,  Böröczky K. ,  Danyi P. ,  Ditrich P. ,  Drávucz Katalin ,  Éltető Ágnes ,  Fülöp 271 R. ,  Guba B. ,  Herczeg T. ,  Hetyei G. ,  Horváth 290 P. ,  Jakab G. ,  Kamocsai A. ,  Károlyi Gy. ,  Kende Ágnes ,  Kerényi I. ,  Kertész Zsuzsa ,  Kiss 563 P. ,  Kokovai Judit ,  Kozák P. ,  Lázár T. ,  Lóczi G. ,  Nacsa J. ,  Nagy 308 G. ,  Nagy 853 B. ,  Óvári 311 G. ,  Rónai Z. ,  Schäffer Z. ,  Szabó 314 L. ,  Szabó E. ,  Szalai J. ,  Szállási Z. ,  Szapanidisz J. ,  Szodfridt Gy. ,  Tranta Beáta ,  Törőcsik J. ,  Vadvári T. ,  Ván 567 P. ,  Zieger B. ,  Zieger Kornélia 
Füzet: 1980/április, 163 - 164. oldal  PDF  |  MathML 
Témakör(ök): Egyenes, Terület, felszín, Gyakorlat, Mértani helyek
Hivatkozás(ok):Feladatok: 1979/november: Gy.1866

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az AB, CD egyeneseket u-val, v-vel és vizsgáljuk először azt az esetet, amikor ezek metszik egymást. Jelöljük ekkor a metszéspontjukat M-mel. Elegendő u-nak, v-nek csak az AB-t, CD-t tartalmazó felét venni, és vizsgálódásunkban az ezek által határolt S szögtartományra szorítkozni, hiszen ebben van az ABCD négy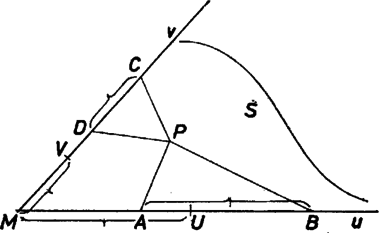szög.

 
 


Mérjük fel e félegyenesekre rendre az MU=AB, MV=DC szakaszokat. Mivel a PAB, PMU háromszögek P-vel szemközti oldala és P-hez tartozó magassága egyenlő, e két háromszög területe is egyenlő. Ugyancsak egyenlő a PCD és PMV háromszögek területe is. Ha P nincs benne az UVM háromszögben, az U, P, V, M csúcsok ebben a sorrendben egy konvex négyszög csúcsai, amelyet akár az UV, akár a PM átlójával kettévághatunk, a kapott részek területének összege mindkét esetben a négyszög területével egyenlő. Ha P az UVM háromszögben van, ezt a PU, PV, PM egyenesek három részre vágják, amelyek területének összege a háromszög területével egyenlő. Most tehát a PMU, PMV háromszögek területének összegét úgy is megkaphatjuk, hogy az UVM háromszög területéből levonjuk az UVP háromszög területét.
Összefoglalva eddigi eredményeinket elmondhatjuk, hogy a PAB és PCD háromszög területének az összege egyenlő az UVM, UVP háromszög területének az összegével vagy különbségével aszerint, hogy UV elválasztja az M, P pontokat, vagy sem. Nyilván igaz ez P helyett E-re is, így P eleve csak akkor tartozhat a vizsgált mértani helyhez, ha UV-nek ugyanazon az oldalán van, mint E. Mivel az UVM háromszög területe nem függ P megválasztásától, P pontosan akkor tartozik a vizsgált mértani helyhez, ha az UVE, UVP háromszögek területe egyenlő. Mivel a két háromszög UV oldala közös, ennek szükséges és elégséges feltétele, hogy P ugyanolyan messze legyen UV-től, mint E, vagyis P rajta legyen az E-n átmenő, UV-vel párhuzamos e egyenesen. (Itt kihasználtuk, hogy E és P az UV-nek ugyanazon az oldalán van.) Mivel a feladat P megválasztását az ABCD négyszög belsejére korlátozza, a vizsgált mértani hely az e egyenesnek a négyszög belsejében levő szakasza.
Ha u és v párhuzamosak, a köztük levő P pontnak tőlük mért u(P), v(P) távolságainak összege független P-től, jelöljük ezt Δ-val. Ha a PAB, PCD háromszögek területének összegéből kivonjuk az EAB, ECD háromszögek területének összegét, a következő különbség felét kapjuk:

[AB⋅u(P)+CD⋅v(P)]-[AB⋅u(E)+CD⋅v(E)]==[AB⋅Δ+(CD-AB)v(P)]-[AB⋅Δ+(CD-AB)v(E)]=(CD-AB)(v(P)-v(E)).


Ebből kiolvasható, hogy a különbség mindig 0, ha CD=AB (vagyis ABCD paralelogramma), ha pedig CD≠AB, akkor csakis v(P)=v(E) esetén 0 a különbség. Ha tehát ABCD paralelogramma, az egész belseje a mértani helyhez tartozik; ha benne AB∥CD, de BC, AD nem párhuzamosak, akkor a mértani hely az AB-vel párhuzamos, E-n átmenő egyenesnek a négyszög belsejébe eső szakasza.