Feladat: Gy.1858 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1980/február, 70 - 71. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Szögfelező egyenes, Egyenes, Gyakorlat, Mértani helyek
Hivatkozás(ok):Feladatok: 1979/október: Gy.1858

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először válasszuk P-t a CBD félköríven. A CPD háromszög nyilván derékszögű és hasonló az ugyancsak derékszögű CEF háromszöghöz, hiszen egy hegyes szögük közös. Mivel P és A a CD átmérő különböző oldalán van, a PA, CD húrok metszik egymást, vagy P a C, D pontok egyikével azonos. Ez utóbbi esetet külön fogjuk vizsgálni. A PA egyenes tehát a CPD háromszög belsejében halad, s mivel A a CD ív felezőpontja, CPA∢=DPA∢, azaz PA belső szögfelezője a CPD háromszögnek. Ekkor felhasználva a szögfelező osztásarányára vonatkozó tételt, mely szerint a szögfelező a szemközti oldalt a közrezáró oldalak arányában osztja, kapjuk, hogy

EFCE=PDPC=EDCE,(1)
ahol az első egyenlőség a hasonló háromszögek megfelelő oldalaira vonatkozik.
 
 

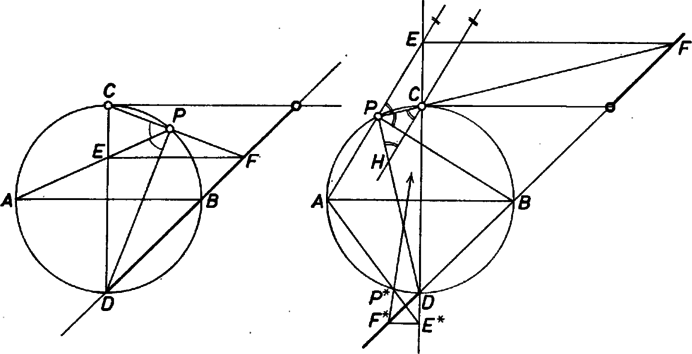Innen adódik, hogy EF=ED, azaz EFD egyenlő szárú derékszögű háromszög. Az F pontok tehát azon az egyenesen sorakoznak, mely a CD átmérővel 45∘-os szöget zár be, ez pedig a BD egyenes. Valóban D is, és B is pontja a mértani helynek. Hiszen ha P=D, akkor PA és DC metszéspontja E, valamint az F pont is azonos D-vel. Ha P=B, akkor E a k középpontja és F megegyezik B-vel.
Ha viszont P a C-be esik, akkor a CP egyenes nincs meghatározva, így nem jön létre F pont. A mértani helyhez tehát nem tartozik hozzá a BD egyenesnek az a pontja, melyet belőle a C=E-n keresztül az AB-vel párhuzamos egyenes metsz ki. Mivel P-t most a CBD köríven vizsgáltuk, mértani helyként a BD egyenesnek csak egy részét kaptuk.
Most vizsgáljuk azokat a P pontokat, melyek a CAD íven vannak. A CPD háromszög most is derékszögű és hasonló CEF-hez. Az (1) aránypár első egyenlősége így most is teljesül. Könnyű belátni, hogy a PA egyenes most külső szögfelezője a CPD háromszögnek, hiszen PB a belső szögfelező és APB∢=90∘, Thalész tétele miatt. Húzzunk párhuzamost a C ponton keresztül az AP szögfelezővel s jelöljük a PD-vel való metszéspontját H-val. Az EPC∢=PCH∢=PHC∢ miatt PH=PC-vel, és a PDE szög száraira felírható a következő aránypár:
PDPH=PDPC=EDECés a hasonlóságbólPDPC=EFEC
így (1) most is teljesül. Emiatt az F pontok most is a BD egyenesen vannak. Mivel most P és A a CD egyenes ugyanazon oldalán van, a CD és AP húrok nem metszik egymást, az AP egyenes C-n, ill. D-n túl metszi a CD-t. Az E és F pontok tehát annál messzebb kerülnek C-től, ill. D-től, minél közelebb van P az A-hoz. Ha P egybeesik A-val, akkor a PA egyenes nem határozható meg, s így nem tartozik hozzá F pont.
A mértani hely tehát egy pontja kivételével a BD egyenes.
Be kell még látnunk, hogy a BD egyenes minden pontja (azt az egyet kivéve) hozzátartozik a mértani helyhez. Vegyünk fel a BD egyenesen egy tetszőleges F pontot. Húzzunk F-en keresztül párhuzamost AB-vel, ez biztosan metszi CD-t. Ez a metszéspont lesz az E pont. E-t összekötve A-val, kapunk a körön egy P pontot. Ennek a P pontnak megfelelő mértani hely pont csak az F lehet, hiszen ez az egyetlen olyan pont, amely az E-n át húzott párhuzamoson is és a BD egyenesen is rajta van.