| Feladat: | Gy.1853 | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Osgyáni Zsuzsanna | ||
| Füzet: | 1980/január, 26 - 27. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai bizonyítások, Derékszögű háromszögek geometriája, Magasságvonal, Logikai műveletek és tulajdonságaik, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1979/szeptember: Gy.1853 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ha egy háromszög valamelyik csúcsát összekötjük a szemközti oldal egyenesének valamelyik pontjával, a keletkező szakasz felezőpontja a választott oldallal párhuzamos középvonalon van. Mivel hegyesszögű háromszögben mindhárom magasságszakasz a háromszög belsejében van, felezőpontjaik rendre az oldalfelező pontok által meghatározott háromszög oldalszakaszain vannak. Emiatt ha ezek a pontok egy egyenesen vannak, a háromszög biztosan nem hegyesszögű. 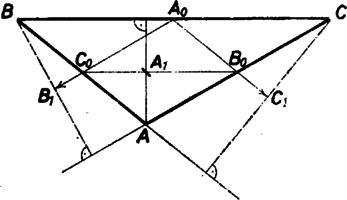 Tompaszögű háromszögben jelöljük a tompaszög csúcsát -val, a másik két csúcsot -vel, -vel, és , , rendre a velük szemközti oldalfelező pontot, , , pedig a megfelelő magasságszakaszok felezőpontját jelölje. Ekkor a -ből, -ből induló magasságszakaszok a egyenes -t tartalmazó oldalán, a háromszögön kívül futnak. Emiatt az , szakaszok -on, illetve -on túli meghosszabbításán van; vagyis a egyenes felőli oldalán. Mivel a szakaszon van, nem lehet rajta a egyenesen. Ezzel beláttuk, hogy ha egy egyenesen van, akkor a háromszög csak derékszögű lehet. Osgyáni Zsuzsanna (Tata, Eötvös J. Gimn., III. o. t.) Megjegyzések. 1. Jelöljük egy adott háromszöggel kapcsolatban -vel azt az állítást, hogy a magasságszakaszok felezőpontjai egy egyenesbe esnek, és -vel azt az állítást, hogy a háromszög derékszögű. Nekünk azt a harmadik állítást kellett igazolnunk, hogy -ből következik . A megoldásban ezt a harmadik állítást úgy igazoltuk, hogy megmutattuk, ha nem igaz, akkor sem igaz. A matematikai logikában járatlan olvasó most biztosan azt mondja, hogy ez hiányos. Esetünkben semmi akadálya belátni, hogy -ből következik , hiszen ha -ban van a derékszög csúcsa, akkor és , valamint és azonosak. Erre azonban elvileg semmi szükség nincs, a legtöbb, amit a bizonyítástól elvárhatunk, az, hogy azt is megmutatta, hogy van olyan háromszög, amelyben igaz. Ez utóbbit úgy mondjuk, hogy ,,nem üres''. 2. Megoldásunk alapja az a szemléletesen világos észrevétel volt, hogy ha egy egyenes egy háromszög valamelyik oldalszakaszát annak valamely belső pontjában metszi, és nem megy át a harmadik csúcson, akkor a másik két oldalszakasz közül pontosan csak az egyiket metszheti belső pontjában. Ez azért van így, mert a harmadik csúcs az első két csúcs közül pontosan csak az egyikkel kerülhet az egyenesnek ugyanarra az oldalára. |