Kezdőlap


Feladat:	Gy.1852	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1980/január, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Aranymetszés, Négyszögek szerkesztése, Sokszögek szimmetriái, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/szeptember: Gy.1852

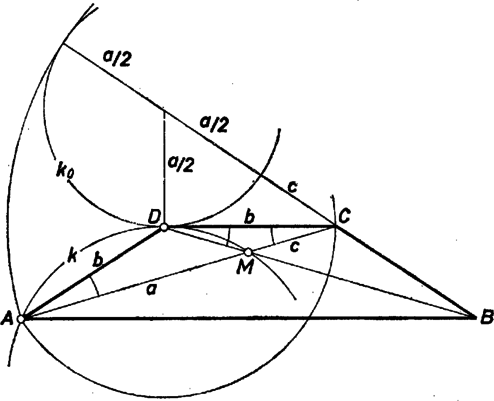
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltevésünk szerint az $A D C$ háromszög egyenlő szárú, és mivel $C$ -nél levő szöge azonos az ugyancsak egyenlő szárú $C D M$ háromszög $C$ -beli szögével, a $D A M$ és $C D M$ szögek is egyenlőek. Emiatt az $A D M$ háromszög köré írható $k$ körnek a $C D$ egyenes érintője, hiszen $D A M ∢$ a $D M$ íven nyugvó kerületi szög, és a $C D M$ szög egyenlő vele. Így a körhöz húzott szelődarabok tétele szerint

\begin{matrix} b^{2} = c (a + c), \end{matrix}

(1)

ahol

c = C M

. Rajzoljunk ezért egy

a / 2

sugarú

k_{0}

kört, és ennek egy

D

pontjában mérjünk fel az érintőre egy

b

hosszúságú szakaszt, ennek végpontja legyen

C

. Kössük össze

C

-t

k_{0}

középpontjával, ennek az egyenesnek

C

-től

k_{0}

-ig tartó darabja éppen

c

hosszúság, hiszen (1) most is igaz, és a szelő

k_{0}

-beli darabja éppen

k_{0}

átmérője. (Mivel

[1]

jobb oldala

c

-nek monoton növő függvénye, csak egy pozitív

c

lehet megoldás.) Ha már ismerjük

c

-t, a

C D M

A D C

háromszögek, végül a keresett

A B C D

trapéz könnyen előállíthatóak.

A szerkesztés akkor végezhető el, ha a

b

c

szakaszokkal egyenlő szárú háromszög szerkeszthető, vagyis

2 c > b

. Mivel (1) ekvivalens a

\begin{matrix} (2 c - b) (2 b + c) = c (3 b - 2 a) \end{matrix}

(2)

egyenlettel, ez olyan pozitív számokra, amelyekre (1) teljesül, akkor és csakis akkor igaz, ha

3 b > 2 a

, ez tehát a szerkeszthetőség feltétele. (Szemléletesen szólva, ha

2 c

már közel van

b

-hez, akkor a

C D M

háromszög nagyon lapos,

M

közel van a

C D

felezőpontjához, és

A M

közel van

1, 5 A D

-hez.)
Ha a

C D M

háromszög megszerkeszthető, a belőle kapott

A B C D

trapéz mindig megfelelő, hiszen amikor a

C D M

háromszöghöz hasonló

A B C

háromszöget megszerkesztjük, abban (1) miatt

A M

hossza éppen

a

lesz. A feladat tehát mindig egyértelműen megoldható, ha

3 b > 2 a

, különben nincs megoldás.

Megjegyzés. Az (1) egyenlet az ún. aranymetszés egyenlete. Erről lapunkban már sokszor esett szó, például az 1979. évi novemberi szám 128. oldalán az F. 2209. megoldása során. Ott említettük, hogy ez a szerkesztés nem más, mint egy szakasz aranymetszés szerinti kettéosztása, ami viszont a szabályos ötszög Euklidésztől származó szerkesztésének az általánosítása. Az érdeklődők erről részletesen lapunk 1977. évi novemberi számában olvashatnak a 135. oldalon (lásd még KÖMAL 1962. májusi szám 201. oldala).