Kezdőlap


Feladat:	Gy.1851	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	1980/január, 23 - 25. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Eltolás, Osztópontok koordinátái, Vektorok lineáris kombinációi, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/szeptember: Gy.1851

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $B + C$ , $A + C$ , $B + A$ pontokat $E$ , $F$ , $G$ -vel. Ez az ,,összeadás'' nem kommutatív, például az $F^{*} = C + A$ pont nem azonos $F$ -fel, hanem annak az $A C$ szakasz felezőpontjára vonatkozó tükörképe: az $A F$ , $C F^{*}$ szakaszok rendre az $A C$ szakasz $60^{\circ}$ -os elforgatásával keletkeznek, de az első esetben $A$ körül, a másodikban $C$ körül forgatunk (1. ábra).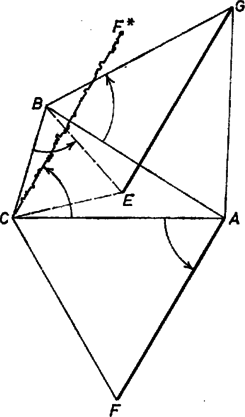

1. ábra

Elforgathatjuk az

A C

szakaszt

B

körül is

60^{\circ}

-kal, ekkor külön el kell forgatnunk az

A

csúcsot

B

körül, így éppen

G

-t kapjuk, és külön forgatni kell

B

körül

C

-t, amikoris

E

-t kapjuk. Mivel a különböző centrumú forgatások párhuzamos és egyállású eredményre vezetnek,

E G

-t

C F^{*}

-ból a

C

-t

E

-be vivő eltolással is megkaphatjuk. Ez viszont

F A

-ból az

F

-et

C

-be vivő eltolással kapható meg, így végül is azt kaptuk, hogy az

F

-et

E

-be vivő eltolás

A

-t

G

-be viszi. Ámde ekkor

F

és

G

A E

szakasz felezőpontjára nézve szimmetrikusan helyezkedik el, és ez épp az, amit bizonyítanunk kellett.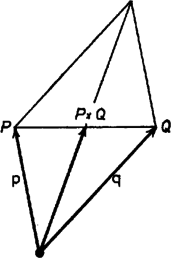

II. megoldás. A sík tetszőleges pontjába mutató helyvektorokat jelöljük rendre a megfelelő kisbetűvel. (A helyvektor olyan vektor, melynek kezdőpontja a sík egy rögzített pontja.) A

P \times Q

művelet eredménye a

P Q

szakasz felezőpontja, s így a vektorok összeadási szabályai szerint ennek a pontnak az

\frac{1}{2} (p + q)

vektor felel meg (2. ábra).

2. ábra

Jelentse

T (u)

azt a vektort, amelyet úgy kapunk meg, hogy az

u

vektort pozitív (az óramutató járásával ellentétes) irányba elfordítjuk

60^{\circ}

-kal. Így a

P + Q

pontba mutató helyvektor

p + T (q-p)

alakba írható (3. ábra). Ezek felhasználásával írjuk fel az (1) alatti műveletek eredményeihez tartozó helyvektorokat.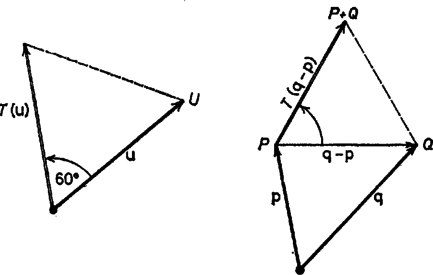

3. ábra

A bal oldal helyvektorának a kétszerese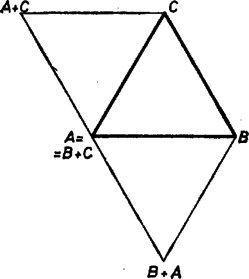

\begin{matrix} a+b + T (c-b), \end{matrix}

a jobb oldal helyvektorának a kétszerese

\begin{matrix} b + T (a-b)+a + T (c-a) . \end{matrix}

Azt kell igazolnunk, hogy ez a két vektor egyenlő. Ehhez elég azt belátnunk, hogy

\begin{matrix} T (c-b) = T (a-b) + T (c-a), \end{matrix}

ahol

a-b

c-a

és

c-b

egy háromszög három oldalának vektorai, mégpedig úgy, hogy az első kettő összege éppen a harmadik. De ebből következik, hogy igaz az egyenlőség, mert két oldal

60^{\circ}

-os elforgatottjának összege egyenlő az összeg

60^{\circ}

-os elforgatottjával. Ezzel igazoltuk az (1) egyenlet helyességét.

Megjegyzések 1. Az I. megoldás szerint dolgozók úgy fejezték be megoldásaikat, hogy az

A

F

E

G

pontok paralelogrammát határoznak meg, tehát a szemközti csúcsokat összekötő szakaszok felezőpontjai egybeesnek. Ez igaz, és megoldásaikat

2

ponttal értékeltük. De megjegyezzük, hogy a megoldásuk hiányos, hiszen nem foglalkoztak azokkal az esetekkel, mikor e négy pont egy egyenesbe esik, pl. ha

A

B

C

egy szabályos háromszög csúcsai (4. ábra).

4. ábra

2. A megoldók egy része a forgásirányt rosszul értelmezte, és olyan szabályos háromszöget szerkesztett, melynek körüljárási iránya megegyezett az óramutató járásával, azaz negatív. A feladat állítása így is igaz, s a bizonyítás hasonlóan megy, ezért az ő megoldásaikat is elfogadtuk.