Kezdőlap


Feladat:	Gy.1844	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Alberti Gábor
Füzet:	1980/január, 18 - 19. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Érintőnégyszögek, Diszkusszió, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/május: Gy.1844

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy négyszög akkor húrnégyszög, ha írható köréje kör. Mivel $3$ pont a kört meghatározza, $D$ -t úgy kell megválasztanunk, hogy rajta legyen az $A$ , $B$ , $C$ pontok által meghatározott körön. E kört mindig meg tudjuk szerkeszteni, ha a $3$ pont nem esik egy egyenesbe.
Mivel a négyszög érintőnégyszög is, ezért szemközti oldalainak összege egyenlő, így $A B + C D = B C + A D$ , azaz átrendezve $| A D - C D | = | A B - B C | = d$ . Mivel $A$ , $B$ , $C$ , $D$ a megadott sorrendben határozza meg a négyszöget, a $D$ pontot a $B$ -t nem tartalmazó $A C$ íven kell keresnünk.
Feltehetjük, hogy $A B > B C$ (ha nem így lenne, betűzzük át a pontokat), akkor az oldalösszegekre fennálló egyenlőség miatt $A D > C D$ , és különbségük ‐ $d$ ‐ ismert.

Tekintsük négyszögünket megszerkesztettnek, és mérjük fel

A

-ból az

A D

szakaszra a

d

távolságot. Jelöljük a végpontját

K

-val. A

C K D

háromszög egyenlő szárú,

D

csúcsnál levő szöge ismert, hiszen az

A B C ∢ = β

-t

180^{\circ}

-ra egészíti ki. Így a

D K C ∢ = \frac{180^{\circ} - (180^{\circ} - β)}{2} = \frac{β}{2}

. Az

A K C

háromszög tehát megszerkeszthető

2

oldala és a nagyobbikkal szemben levő szöge ismeretében.
A négyszög szerkesztésének menete a következő: az

A

B

C

pontok köré kört szerkesztünk, majd az

A C

oldal fölé

180^{\circ} - \frac{β}{2}

látószögű kört. Ezt

A

-ból

d

távolsággal elmetszve kapjuk a

K

pontot. Az

A K

egyenes metszi ki a körből

D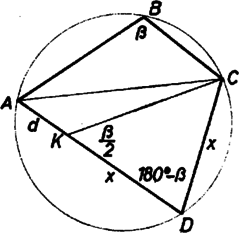

-t.

Az így kapott négyszög valóban húrnégyszög, de egyben érintőnégyszög is. Könnyen kiszámolhatjuk a

D C K ∢

-t

\begin{matrix} D C K ∢ = 180^{\circ} - (\frac{β}{2} + 180^{\circ} - β) = \frac{β}{2} . \end{matrix}

C D K

háromszögben

C D = D K = x

, így

A B + C D = A B + x

B C + A D = B C + d + x

, és mivel

A B = B C + d

, a két összeg valóban egyenlő. Ez pedig szükséges és elégséges feltétele annak, hogy egy négyszög érintőnégyszög legyen.
A feladatnak mindig van megoldása, ha

A

B

C

nem esik egy egyenesbe, és mindig

1

megoldása van, mivel

d = | A B - B C | < A C

mindig teljesül a háromszög oldalaira fennálló összefüggés miatt. Ha

A B = B C

, akkor a húrnégyszög deltoid, és

D

-t a

B

-ből az

A C

-ra állított merőleges metszi ki a körből.

Alberti Gábor (Budapest, Árpád Gimn., I. o. t.)