Kezdőlap


Feladat:	Gy.1836	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1980/május, 208 - 209. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Érintőnégyszögek, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/április: Gy.1836

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a beírt kör középpontját $O$ -val, az oldalakkal való érintési pontjait $E_{1}, E_{2}, E_{3}, E_{4}$ -gyel, ahol $E_{1}$ az $A B_{1}, E_{2}$ a $B C$ stb. oldalon van, a négyszög szögeit $α, β, γ$ és 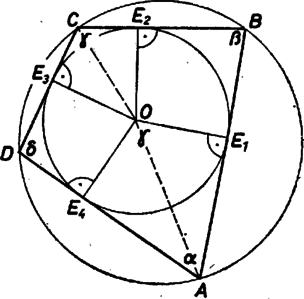$δ$ -val.

A most bevezetett jelöléseket felhasználva az állítás a következő alakban írható:

\begin{matrix} \frac{A E_{1}}{E_{1} B} = \frac{D E_{3}}{E_{3} C} . \end{matrix}

(1)

Ezt kell bizonyítanunk.
Nyilván az

A E_{1} O, B E_{2} O, C E_{3} O, D E_{4} O

szögek derékszögek, s ezért a négy kis négyszög mindegyikében a szemközti szögek összege

180^{\circ}

, pl. az

E_{4} A E_{1} O

négyszögben

E_{4} A E_{1} ∢ + E_{1} O E_{4} ∢ = 180^{\circ}

. Mivel

A B C D

húrnégyszög, az

E_{4} A E_{1} ∢ = α

szöget a

C

csúcsnál levő

γ

szög is

180^{\circ}

-ra egészíti ki, amiből következik, hogy

E_{1} O E_{4} ∢ = γ

.
Az

A E_{1} O E_{4}

és

O E_{2} C E_{3}

négyszög szögei megegyeznek, ebből azonban még nem következik, hogy hasonlók. Ellenben ha az átlókat meghúzzuk ‐ mivel a négyszögek deltoidok ‐ az így kapott szögek is egyenlők lesznek.
Ebből már következik, hogy a két négyszög hasonló, és így megfelelő oldalaik arányosak, azaz

\begin{matrix} \frac{A E_{1}}{O E_{2}} = \frac{E_{4} O}{E_{3} C}, \end{matrix}

ahonnan

A E_{1} \cdot E_{3} C = E_{4} O \cdot O E_{2}

. Hasonlóan az

E_{1} B E_{2} O

és

E_{4} O E_{3} D

négyszögekben

\begin{matrix} \frac{E_{1} B}{E_{4} O} = \frac{O E_{2}}{D E_{3}}, \end{matrix}

ahonnan

E_{1} B \cdot D E_{3} = O E_{2} \cdot E_{4} O

. A két egyenlőségből

A E_{1} \cdot E_{3} C = E_{1} B \cdot D E_{3}

, amit átrendezve kapjuk az állítást.

Megjegyzés. A feladat szövege külön nem mondta ki, hogy a négyszög konvex. Ez azonban következik abból, hogy húrnégyszög, s így a négyszögnek nem lehet pontja egyetlen oldal meghosszabbításán sem. Az érintőnégyszög definíciójából viszont az következik, hogy az érintőkör az oldalakat és nem azok meghosszabbítását érinti. Ha az utóbbi esetet megengednénk, akkor úgynevezett hurkolt négyszöget kapnánk, amilyet az ábra mutat. Könnyen látható, hogy az ilyen esetekben a feladat állítása nyilvánvaló.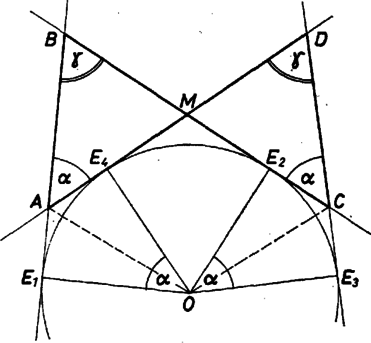

Mivel

A B C D

feltétel szerint húrnégyszög, azaz írható köréje kör,

B A D ∢ = B C D ∢ = α, A B C ∢ = A D C ∢ = γ

. Az

A E_{1} O

és

C E_{3} O

háromszögek egybevágók,

O E_{1} = O E_{3}

, és a szögek egyenlősége miatt ezért

A E_{1} = A E_{4} = C E_{3} = C E_{2}

. Jelöljük

A D

és

B C

metszéspontját

M

-mel.

M E_{4} = M E_{2}

, s az előzőkből

M C = M A

adódik. Az

A B C D

négyszög tehát szimmetrikus trapéz, s így

B A = D C

. (1) tehát most is teljesül.