Feladat: Gy.1818 Korcsoport: 14-15 Nehézségi fok: könnyű
Füzet: 1979/október, 71. oldal  PDF  |  MathML 
Témakör(ök): Vetítések, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Négyzetek, Gyakorlat
Hivatkozás(ok):Feladatok: 1979/február: Gy.1818

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Messe a DM egyenes az AB egyenest az N pontban. Könynyen belátható, hogy DMC▵≅MBN▵, így BN=DC=AB. Az APN∢=90∘, így a Thalész‐tétel megfordítása értelmében P rajta van a B középpontú, AB sugarú körön. Így AB és PB is sugarak, tehát egyenlők (1. ábra).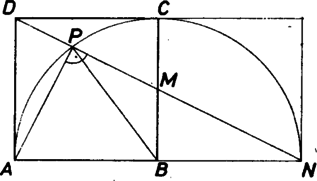

 

 
1. ábra

 

II. megoldás. Húzzunk párhuzamost B-n keresztül DM-mel, az AP-vel való metszéspont legyen E, AD-vel való M', az A-n átmenő, DM-mel párhuzamos egyenes metszéspontja a BC egyenessel M''. Ekkor kapjuk az AM''MD paralelogrammát, amelynek M'B középvonala lesz, hiszen MB fele AD-nek és M'B∥DM∥AM''. A paralelogramma AP magasságát a középvonal felezi. Ez azt jelenti, hogy ABP háromszögben EB magasság egyben felezi az AP oldalt, vagyis a háromszög egyenlő szárú, AB=BP (2. 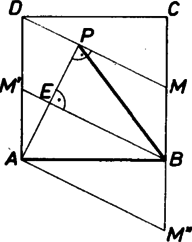ábra).
 

 
2. ábra

 

III. megoldás. A BAM és CDM egybevágó háromszögben BAM∢=CDM∢=α. A DPA háromszögben PAD∢=CDM∢=α, megfelelő száraik merőlegesek egymásra és mindkettő kisebb mint 90∘. Emiatt BAP∢=90∘-α.
AMB és APM közös átfogójú derékszögű háromszögek, az AM átfogójuk fölé írt Thalész‐kör átmegy a B és P ponton is. Ezért BPM∢=BAM∢=α, ugyanazon húrhoz tartozó kerületi szögek, amiből APB∢=90∘-α következik, azaz valóban 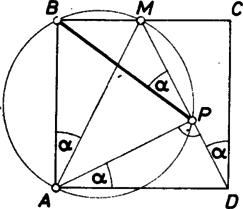AB=PB.
 

 
3. ábra