Kezdőlap


Feladat:	Gy.1810	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	1979/május, 210 - 211. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Körülírt kör, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/január: Gy.1810

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bizonyítandó állítást az $M' A C$ , $M' B C$ háromszögekre felírva

\begin{matrix} M' A^{2} + A C^{2} + C M'^{2} = M' B^{2} + B C^{2} + C M'^{2}, \end{matrix}

elegendő azt belátnunk, hogy

\begin{matrix} M' A^{2} + A C^{2} = M' B^{2} + B C^{2} . \end{matrix}

(1)

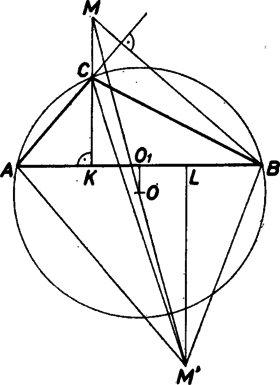Jelöljük az

M

O

M'

pontoknak az

A B

egyenesre eső merőleges vetületét rendre

K

O_{1}

és

L

-lel.
Az

A C K

, valamint

L B M'

derékszögű háromszögekben

\begin{matrix} A C^{2} = A K^{2} + K C^{2}, \end{matrix}

(2)

ill.

\begin{matrix} M' B^{2} = M' L^{2} + L B^{2} . \end{matrix}

Továbbá az

A L M'

és

B C K

háromszögekben

\begin{matrix} M' A^{2} = M' L^{2} + A L^{2}; \end{matrix}

(3)

\begin{matrix} B C^{2} = K C^{2} + K B^{2} . \end{matrix}

Adjuk össze a (2) és (3) alatti két-két egyenlőség megfelelő oldalait. Kapjuk, hogy

\begin{matrix} A C^{2} + M' A^{2} = A K^{2} + K C^{2} + M' L^{2} + A L^{2}, \end{matrix}

ill.

\begin{matrix} M' B^{2} + B C^{2} = M' L^{2} + L B^{2} + K C^{2} + K B^{2} . \end{matrix}

Az egyenletek bal oldalain éppen a kívánt (1) összefüggés két oldala áll, s mert

O_{1}

felezi

A B

-t és

M O = O M'

miatt

K O_{1} = O_{1} L

, így az

A K = L B

és

A L = K B

egyenlőség is fennáll. Emiatt a jobb oldalon álló kifejezések is egyenlők.
Mivel a két háromszöget tetszőlegesen választottuk, az állítás bármely kettőre igaz. Ezzel igazoltuk a feladat állítását.