Feladat: Gy.1796 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1979/március, 118 - 119. oldal  PDF  |  MathML 
Témakör(ök): Középpontos tükrözés, Egyenlő szárú háromszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1978/november: Gy.1796

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük azt a B körüli 60∘-os forgatást, amely a C pontot Q-ba viszi át. Majd fordítsuk el a CB szakaszt A körül 60∘-os szöggel, az előző forgatással egyező irányba, B elfordítottja B1, C-é C1. BQ és a B1C1 a BC szakasznak ugyanazon irányban, ugyanakkora szöggel elfordított képei ‐ csak a forgatás centruma előbb a B, majd az A pont ‐, ezért párhuzamosak és egyirányúak, a BQC1B1 négyszög paralelogramma.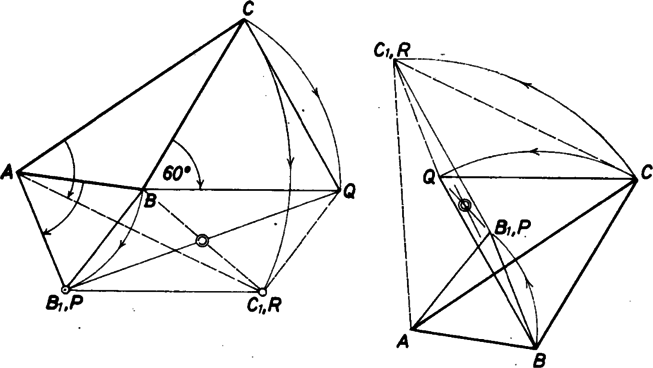

 

 

Ha az ABP szabályos háromszög körüljárását ugyanolyan irányúnak vettük, mint a BCQ  háromszögét ‐ más szóval: ha P-t és Q-t egyformán kifelé vagy egyformán befelé szerkesztettük az AB, ill. a BC oldal fölé ‐, akkor B1 nyilván azonos P-vel. Ebből következik, hogy C1 ‐ mint a BQC1P paralelogrammában B-vel szemben levő csúcs, vagyis B tükörképe a másik átló QP felezőpontjára ‐ azonos a feladat szerint vizsgálandó R ponttal. Ámde szerkesztése szerint C1 szabályos háromszöget alkot A-val és C-vel, tehát ez áll (a közvetlenül megszerkesztett) R-re is. ‐Azt is kaptuk ezzel, hogy az ACR háromszög körüljárása egyező ABP és BCQ közös körüljárási irányával.
Végül vizsgáljuk meg azt a lehetőséget, mikor az ABP háromszöget a BCQ-val ellentétes körüljárásúnak vesszük, más szóval az egyiket kifelé, a másikat befelé rajzoljuk az illető oldalra. Ilyenkor a fönti B1 pont nem azonos P-vel, a bizonyítás erre az esetre nem alkalmazható. Sőt ebben az esetben az állítás nem is igaz. Elég egyetlen ellenpélda ennek belátására. Legyen maga az ABC háromszög is szabályos, a BCQ háromszöget kifelé, ABP-t befelé illesszük oda; így  P azonos C-vel, R pedig az A tükörképe C-re nézve, tehát a kérdéses 3 pont nem alkot szabályos háromszöget.