Kezdőlap


Feladat:	Gy.1778	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1979/január, 17 - 18. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Derékszögű háromszögek geometriája, Paralelogrammák, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1978/szeptember: Gy.1778

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $P$ és $Q$ pontokon keresztül húzzunk párhuzamosokat az $A C$ befogóval. Jelöljük a párhuzamosok talppontjait a $C B$ -n rendre $P_{1}$ , $Q_{1}$ -gyel. Nyilván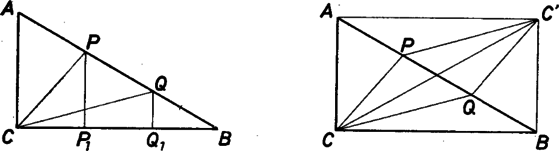

\begin{matrix} P P_{1} = \frac{2}{3} A C, Q Q_{1} = \frac{1}{3} A C, C P_{1} = \frac{1}{3} C B, C Q_{1} = \frac{2}{3} C B . \end{matrix}

C P

, ill.

C Q

távolságokat a

C P P_{1}

, ill.

C Q Q_{1}

háromszögekből Pitagorasz-tétel felhasználásával kapjuk:

\begin{matrix} C P^{2} = C P_{1}^{2} + P P_{1}^{2} = {(\frac{1}{3} C B)}^{2} + {(\frac{2}{3} A C)}^{2}, \end{matrix}

ill.

\begin{matrix} C Q^{2} = C Q_{1}^{2} + Q Q_{1}^{2} = {(\frac{2}{3} C B)}^{2} + {(\frac{1}{3} A C)}^{2} . \end{matrix}

És mivel

P Q = \frac{1}{3} A B

, a keresett összeg

\begin{matrix} {(\frac{1}{3} C B)}^{2} + {(\frac{2}{3} A C)}^{2} + {(\frac{2}{3} C B)}^{2} + {(\frac{1}{3} A C)}^{2} + {(\frac{1}{3} A B)}^{2} = \\ = \frac{5}{9} (A C^{2} + C B^{2}) + \frac{1}{9} A B^{2} = \frac{2}{3} A B^{2}, \end{matrix}

hiszen

A C^{2} + C B^{2} = A B^{2}

II. megoldás. Tükrözzük a háromszöget az

A B

szakasz felezőpontjára. A tükrözéskor

A

és

B

pontok helyzete felcserélődik,

C

tükörképe

C'

, és a tükrözésből következik, hogy

A C' B C

négyszög téglalap. Továbbá

C P C' Q

paralelogramma, hiszen átlói felezik egymást. Alkalmazzuk rá azt a kevésbé ismert tételt, mely szerint a paralelogramma oldalainak négyzetösszege egyenlő az átlók négyzetösszegével. (Az állítást pl. a Pitagorász-tétel felhasználásával igazolhatjuk.)

Eszerint

\begin{matrix} 2 C P^{2} + 2 C Q^{2} = P Q^{2} + C C'^{2}, s mivel P Q = \frac{1}{3} A B és C C' = A B, \\ C P^{2} + C Q^{2} = \frac{1}{2} [{(\frac{1}{3} A B)}^{2} + A B^{2}] = \frac{5}{9} A B^{2}, \end{matrix}

amiből következik az állítás.