Kezdőlap


Feladat:	Gy.1773	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csordás András
Füzet:	1978/december, 213 - 215. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középvonal, Diszkusszió, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1978/május: Gy.1773

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk úgy a jelölést, hogy az $A B C D$ paralelogrammában $A D > D C$ , az átlók által bezárt szög $φ$ , $A D - D C = d > 0,$ és legyen adva az $A C$ átló. Jelöljük az átlók metszéspontját $O$ -val.

1. ábra

Mivel ismerjük az átlók hajlásszögét, meg tudjuk húzni a

B D

átló egyenesét is. Mérjük fel az

A D

oldalra a

D E = D C

távolságot. A

C

E

pontokon átmenő egyenes messe a

B D

átló egyenesét a

Q

pontban. A

C D E

egyenlő szárú háromszögben húzzuk meg a

C E

oldalhoz tartozó magasságot, és jelöljük a talppontját

P

-vel. Mivel

P

felezi

E C

-t és

O

felezi

A C

-t,

O P ∥ A E

és

O P = \frac{1}{2} A E = \frac{1}{2} d

. Vetítsük a

C

pontot merőlegesen a

B D

-re, s jelöljük a vetületét

C'

-vel. A

C D C'

és

C D P

közös átfogójú derékszögű háromszögek,

P C D C'

tehát húrnégyszög. Ha

C'

C D'

ugyanazon oldalára esik, mint

P

, akkor

P C D ∢ + P C' D ∢ = 180^{\circ}

(1. ábra), s ezért

P C D ∢ = P C' O ∢

. Ha

P

és

C'

C D

szakasz ellenkező oldalán van (2. ábra), akkor

D C P ∢ = D C' P ∢

egyenlő húrhoz tartozó kerületi szögek. Továbbá

D C P ∢ = D E P ∢ = E P O ∢

. Mindkét esetben az

O P C'

és

O P Q

háromszögek hasonlók (két szögük egyenlő), és így

\begin{matrix} {O P}^{2} = O Q \cdot O C' . \end{matrix}

(1)

O P

és

O C'

szakaszok hosszát ismerjük, s így

O Q

távolságot meg tudjuk szerkeszteni.

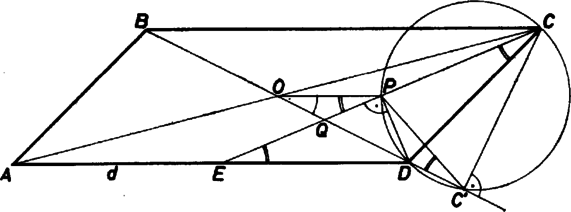2. ábra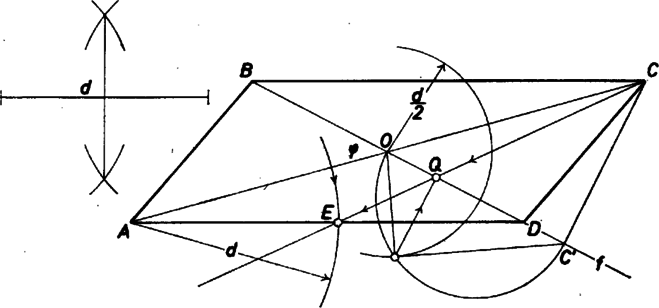

3. ábra

Ennek alapján a szerkesztést a következőképpen végezhetjük el (3. ábra).
Felvesszük az

A C

szakaszt, az

O

felezőpontján át meghúzzuk a

B D

átló

f

egyenesét, mely vele az adott

φ

szöget zárja be. A

C

pontot levetítjük

f

-re és

O C'

és

O P = \frac{1}{2} d

ismeretében

(1)

felhasználásával megszerkesztjük az

O Q

távolságot. Majd

A

körül egy

d

sugarú kört rajzolunk. Ahol a kör metszi a

C Q

egyenest, ott kapjuk az

E

, ill.

E'

pontot. A körnek az egyenessel általában két metszéspontja lesz. Az ezeket

A

-val összekötő egyenesek metszik ki

f

-ből a paralelogramma hiányzó csúcsait, az

1

. ábra szerinti

A E'

B

csúcsot, hiszen

E C D ∢ = C E D ∢ = A E E' ∢ = E E' A ∢

miatt

E' A ∥ C D

. A szerkesztés menetéből következik, hogy az

A B C D

paralelogramma eleget tesz a feltételnek.
A megoldhatóság feltétele, hogy az

A

körüli,

d

sugarú kör két különböző pontban messe az

O Q

egyenest. Nyilvánvaló továbbá, hogy a háromszög-egyenlőtlenség miatt az is szükséges, hogy

d < A C

legyen. Bővebb diszkussziót nem végezhetünk.
Tekintsük végül az adathármasnak azt a különleges, esetét, ha

φ = 90^{\circ}

. Ekkor

C'

O

-ba esik, szerkesztésünk nem hajtható végre, de az átlók merőlegességéből tüstént következik, hogy a paralelogramma csak rombusz lehetne. Így

d = 0

mellett a feladat határozatlan,

d > 0

mellett pedig az adathármas ellentmondó. (

d = 0

-ból indulva viszont az következik, hogy csak

φ = 90^{\circ}

lehet.)
A szerkesztés helyességét a következőképpen igazolhatjuk. Miután megszerkesztettük a

C Q

egyenest a fent leírt módon, s elmetszettük az

A

pont körüli

d

sugarú körrel, húzzunk párhuzamost az

O

ponton keresztül az

A E

-vel. A kapott

P

pont nyilván felezi az

E C

távolságot. A mértani közép tulajdonságából következik, hogy

O P Q ∢ = P C' Q ∢

, valamint a párhuzamosság miatt

O P Q ∢ = A E E' ∢

P

-ben állítsunk merőlegest

E C

-re, s messe ez az

f

-et

D'

-ben.

E C D'

háromszög egyenlő szárú,

E C D' ∢ = C E D' ∢

, továbbá

C P C' D'

négyszög húrnégyszög, s ezért

P C D' ∢ = P C' Q ∢

. Messe az

A E

egyenes az

f

egyenest

D

-ben, az

A E E' ∢ = C E D ∢

. S mivel

C E D'

és

C E D

szögek nagysága megegyezik és egyik száruk közös, kell hogy a

D

egybeessen

D'

-vel. Az

A B C D

idom paralelogramma ‐ hiszen

A E' ∥ C D

, s mivel

O

felezi

A C

-t, így kell hogy felezze

B D

-t is ‐, s eleget tesz az előírt feltételeknek.

Csordás András (Esztergom, Dobó K. Gimn.)