Kezdőlap


Feladat:	Gy.1765	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gát György
Füzet:	1978/november, 145 - 146. oldal		PDF \| MathML
Témakör(ök):	Kocka, Gömb és részei, Térgeometriai számítások trigonometria nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1978/április: Gy.1765

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A legkisebb olyan gömb, amelynek van közös pontja a lapátlókkal az, amelyik éppen érinti a négyzeteket a lapközéppontjukban. Ennek a gömbnek a sugara $1 / 2$ , és az így kapott konvex test az oktaéder, melyet $8$ db szabályos háromszöglap határol.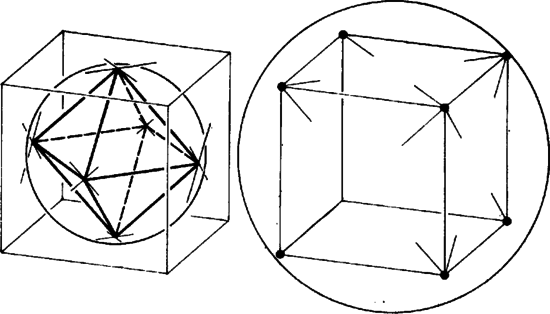
A legnagyobb gömb, amelynek még van közös pontja a lapátlókkal, a kocka köré írt gömb. A metszéspontok az átlók végpontjai, azaz a kapott konvex test a kiindulási kocka. A gömb sugara a kocka testátlójának fele, $\frac{\sqrt[]{3}}{2}$ .

Vizsgáljuk most azt az esetet, amikor a gömb a lapátlókat két ‐ a végpontjaiktól különböző ‐ pontban metszi. Bármekkora is a gömb sugara, középpontja (mely egyben a kockának is középpontja) bármely lap középpontjától

1 / 2

távolságra van. A kocka és a gömb szimmetriájából következik, hogy minden egyes lapon

4

metszéspont jön létre. Vizsgáljuk meg azt a konvex testet, amelyet a metszéspontok meghatároznak.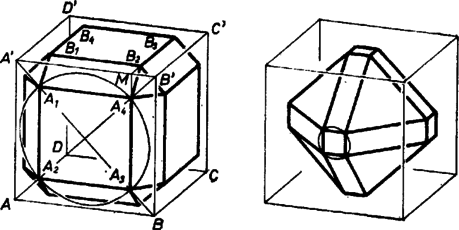

Jelölje

A

B

C

D

a kocka alaplapját pozitív forgási irány szerint felsorolva és

A'

B'

C'

D'

rendre az

A

B

C

D

feletti csúcsokat. Az

A B B' A'

, ill.

A'

B'

C'

D'

szomszédos lapokon a gömb által kimetszett négyzetek csúcsai

A_{1}

A_{2}

A_{3}

A_{4}

, ill.

B_{1}

B_{2}

B_{3}

B_{4}

ugyancsak pozitív forgásirány szerint megadva úgy, hogy

A_{1} A_{4} ∥ A' B'

, ill.

B_{1} B_{2} ∥ A' B'

és

A_{1}

, ill.

B_{1}

közelebb van

A' B'

-hoz, mint

A_{2}

, ill.

B_{4}

.
A szimmetria miatt a

B_{2}

pontnak a

C' B' B

síktól való távolsága ugyanannyi, mint az

A_{4}

ponté, azaz

B_{2} A_{4} ∥ C' B' B

síkkal.

B_{1} B_{2} ∥ A' B' ∥ A_{1} A_{4}

, s mivel

A' B'

merőleges

C' B' B

síkra, így merőleges

A_{4} B_{2}

egyenesre is, azaz az

A_{1} A_{4} B_{2} B_{1}

négyszög általában téglalap. A konvex testet tehát

6

db négyzet,

12

db téglalap és

8

db háromszög határolja. Mivel a kocka testátlói körüli

120^{\circ}

-os forgatás a kockát is, a gömböt is önmagába viszi át, ez utóbbiak szabályosak.
Feladatunkban annak a gömbnek a sugarát keressük, amellyel elmetszve a kockát, a téglalap oldalai egyenlők lesznek.
Jelöljük a feltételnek eleget tevő gömb sugarát

r

-rel, s fejezzük ki a kockalapon keletkezett négyzetek oldalát

r

függvényeként. A négyzet átlójának felére

\sqrt[]{r^{2} - {(\frac{1}{2})}^{2}}

adódik, ahonnan a négyzet oldala

\begin{matrix} a = \frac{2}{\sqrt[]{2}} \sqrt[]{r^{2} - {(\frac{1}{2})}^{2}} = \sqrt[]{2 r^{2} - \frac{1}{2}} . \end{matrix}

Ennyivel kell egyenlőnek lennie az

A_{4} B_{2}

szakasznak is. Az

A_{4} B_{2}

szakasz hosszát ugyancsak Pitagorász tétele segítségével határozhatjuk meg. Fektessünk az

A_{4} B_{2}

egyenesre egy síkot, mely merőleges

A' B'

-re, s jelöljük az

A' B'

-vel való metszéspontját

M

-mel. Az

A_{4} M B_{2}

egyenlő szárú derékszögű háromszögben

\begin{matrix} M B_{2} = M A_{4} és A_{4} B_{2} = \sqrt[]{2} \cdot M B_{2} = a, \end{matrix}

ahonnan

\begin{matrix} M B_{2} = \frac{a}{\sqrt[]{2}} . \end{matrix}

B_{2} M A_{4}

sík a kocka fedőlapját a

B' C'

éllel párhuzamos egyenesben metszi, így

\begin{matrix} a + 2 \cdot \frac{a}{\sqrt[]{2}} = 1 és a = \sqrt[]{2 r^{2} - \frac{1}{2}} \end{matrix}

összefüggések felhasználásával a

\begin{matrix} (\sqrt[]{2} + 1) \sqrt[]{2 r^{2} - \frac{1}{2}} = 1 \end{matrix}

egyenlethez jutunk. Innen mivel

r > 0

, ezért az

r = \sqrt[]{\frac{7}{4} - \sqrt[]{2}} = 0, 579

értéket kapjuk a keresett gömb sugarára.

Gát György (Esztergom, Dobó K. Gimn., II. o. t.)