Kezdőlap


Feladat:	Gy.1762	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1978/november, 143 - 144. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Beírt kör középpontja, Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1978/április: Gy.1762

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög csúcsait és szögeit a szokásos módon, a szögfelezők metszéspontját $M$ -mel, a körülírt kört $k$ -val. Válasszuk ki a háromszög két csúcsát, legyen ez pl. $A$ és $C$ . Jelöljük az $A$ , $M$ , $C$ pontok köré írt kört $k_{1}$ -gyel, középpontját $O_{1}$ -gyel. Azt állítjuk, hogy $O_{1}$ rajta van a $k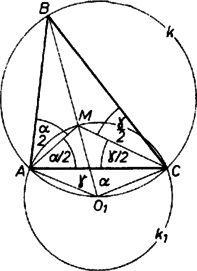$ körön.

k_{1}

körben

M O_{1} A ∢ = 2 M C A ∢ = γ

, mert egyenlő íven nyugvó kerületi, ill. középponti szögek. Hasonlóan

M O_{1} C ∢ = 2 M A C ∢ = α

. Az

A B C O_{1}

négyszögben

B ∢ = β

, s így két szemközti szögének összege

α + β + γ = 180^{\circ}

, azaz

A B C O_{1}

húrnégyszög. Ami éppen azt jelenti, hogy

O_{1}

rajta van a

k

körön.

Megjegyzések. 1. Mivel

A O_{1} M ∢ = γ = A O_{1} B ∢

M

rajta van

B O_{1}

-en. Ez azt jelenti, hogy

O_{1}

-et a

B

-beli szögfelező metszi ki

k

-ból,

O_{1}

A C

ív felezőpontja.
2. Az állítás akkor is igaz, ha két külső szögfelező és a harmadik csúcsból induló belső felező közös pontját vesszük a kör harmadik pontjának.