Feladat: Gy.1761 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Ács J. ,  Arató M. ,  Bajnok B. ,  Baumann O. ,  Beleznay F. ,  Bereznai M. ,  Brachna L. ,  Bölcsföldi L. ,  Böröczky K. ,  Csató L. ,  Csordás A. ,  Czifra A. ,  Dénes L. ,  Elek Gábor ,  Erdélyi T. ,  Gaál I. ,  Gát Gy. ,  Hacker Erika ,  Hajnal P. ,  Hetyei G. ,  Horváth 169 T. ,  Jordán J. ,  Kántor S. ,  Karakas J. ,  Károlyi Gy. ,  Katona I. ,  Kiss 352 Gy. ,  Koppány Zs. ,  Lengvárszky Zs. ,  Lévai P. ,  Madarász J. ,  Mala J. ,  Nagy 111 Cs. ,  Nagy 647 G. ,  Náray Zsófia ,  Oláh K. ,  Papp 412 Zs. ,  Pintér 395 F. ,  Rátz Á. ,  Ruisz T. ,  Schwarcz P. ,  Seres I. ,  Simonyi G. ,  Szabó 200 Ágnes ,  Tálas Cs. ,  Tóth J. ,  Tranta Beáta ,  Varga Lívia ,  Winkler R. 
Füzet: 1978/november, 142 - 143. oldal  PDF  |  MathML 
Témakör(ök): Irracionális számok és tulajdonságaik, Algebrai átalakítások, Gyakorlat, Törtfüggvények
Hivatkozás(ok):Feladatok: 1978/április: Gy.1761

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük x-et z-vel, és alakítsuk át a szóban forgó két függvény különbségét.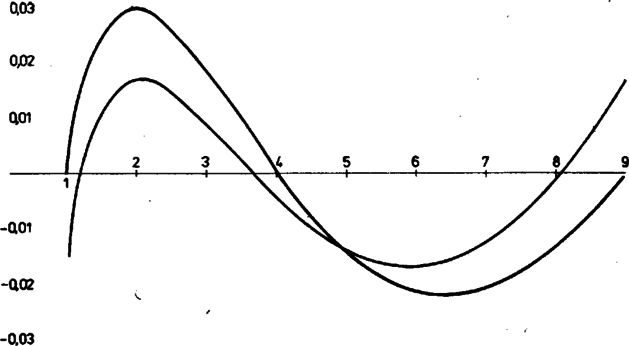

D=z-6z2+6z2+11=(z-1)(z-2)(z-3)z2+11.
Itt a nevező mindig nagyobb 10-nél, emiatt elég belátnunk, hogy a számláló abszolút értéke legfeljebb 1/2. Ha 1≤x≤4, akkor 1≤z≤2, és a számlálóban
0≤(z-1)(2-z)=14-(z-32)2≤14,0<3-z≤2,
tehát a számláló nem negatív, és értéke valóban legfeljebb 1/2. Ha pedig 4≤x≤9, akkor 2≤z≤3, és a számlálóban
0<z-1≤2,0≤(z-2)(3-z)=14-(z-52)2≤14,
tehát most a számláló nem pozitív, és abszolút értéke ismét legfeljebb 1/2.
 
 

Elek Gábor (Budapest, Eötvös J. Gimn., I. o. t.)

 
Megjegyzés. Az (ax+b)/(cx+d) alakú függvények közül x-et az 1≤x≤9 intervallumban legjobban az (5,86863...x+6,06458...)/(x+10,73727...) közelíti meg, a két függvény eltérése kisebb, mint 0,016695.... Ennek, valamint a feladatban megadott függvénynek x-től való eltérését rajzoltuk fel az ábrán.
Az ilyen jellegű, ún. racionális törtfüggvénnyel való közelítések fontos feladatot töltenek be a számológépek programozásánál, így például a négyzetgyökvonás rutinjában (amit a zsebszámológépek esetében a gépbe ,,beégettek'' vagy ,,behuzaloztak'') a Newton‐Raphson iteráció kezdőértékét (lásd ez évi májusi számunk 220. oldalán) ily módon számítják. S minél pontosabb a kezdőérték, annál kevesebb iterációs lépésre van szükség, sőt a szükséges iterációs lépések számát is meg lehet előre határozni, függetlenül az x értékétől.