Kezdőlap


Feladat:	Gy.1756	Korcsoport: 14-15	Nehézségi fok: könnyű
Füzet:	1978/október, 67. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1978/március: Gy.1756

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a kerületi szögek tételéből következik az alábbi állítás helyessége. Azt fogjuk felhasználni, hogy két egymást metsző kör egyik metszéspontján át húzott szelőknek a két kör által lefedett szakasza a másik metszéspontból állandó szög alatt látszik. (Lásd I. o. tankönyv 313. o. 51. feladat.)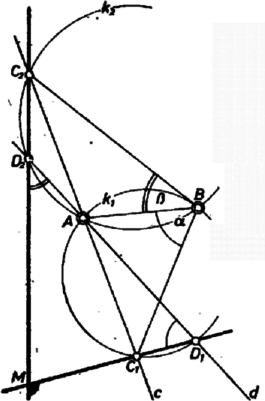
Jelöljük a $C_{1} D_{1}, C_{2} D_{2}$ egyenesek metszéspontját $M$ -mel és legyen $C_{1} B A ∢ = α, A B C_{2} ∢ = β$ . (1. ábra). Az $A D_{2} C_{2} B$ húrnégyszög, s így $A D_{2} M ∢ = 180^{\circ}$ $- (180^{\circ} - β) = β$ . A $D_{1}$ csúcsnál levő kerületi szög $α$ -val egyenlő. $D_{1} M D_{2}$ háromszögben tehát $D_{1} M D_{2} ∢ = 180^{\circ} - (α + β)$ . Mivel $α + β$ állandó, ezért az $M$ szög is állandó, tehát nem függ az egyenesek választásától.

1. ábra

Megjegyzés. Bizonyításunk olyan esetre érvényes, amelyben a

C_{1} C_{2}, D_{1} D_{2}

szakaszok mindegyikére nézve az

A

belső pont. Ajánljuk az olvasónak a- szükséges módosítások átgondolására a 2. ábrát, amelyen

A

mindkét szakaszra nézve külső pont, továbbá hogy a ,,vegyes'' helyzetet mutató 3. ábrán gondolják át a bizonyítást

c

és

d

szerepei kiosztásának mindkét lehetősége szerint. (Figyeljük meg: a

C_{1}, C_{2}

pontokat szögek jelölésére használtuk fel, a

D_{1}, D_{2}

pont pár révén pedig a kérdéses szögek egyikét számítottuk.)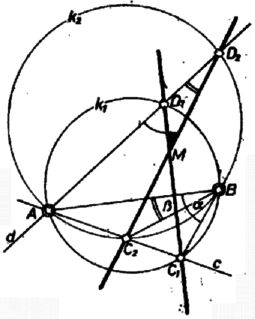

2. ábra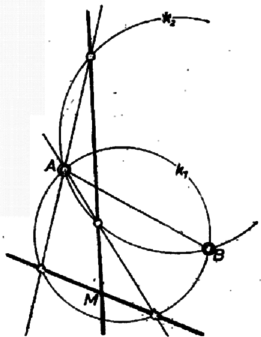

3. ábra