Kezdőlap


Feladat:	Gy.1749	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1978/október, 65. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Térgeometriai számítások trigonometria nélkül, Szabályos sokszögek geometriája, Gyakorlat, Mértani közép
Hivatkozás(ok):	Feladatok: 1978/február: Gy.1749

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $C D$ oldal felezőpontját $F$ -fel. Ha $A M$ merőleges a $C D M$ síkra, merőleges a benne levő $F M$ egyenesre is. Megfordítva, ha $M$ -et úgy választjuk meg, hogy az $A F M$ háromszög derékszögű legyen, akkor $A M$ merőleges lesz az egész $C D M$ síkra, hiszen $F M$ -en kívül a $C D$ egyenesre is merőleges. Az $A F M$ háromszög viszont ismert tétel szerint akkor és csakis akkor derékszögű $M$ -ben, ha a magassága az átfogó két, általa létrehozott darabjának mértani közepe. Ha tehát $O$ az $A B C D E$ ötszög centruma, akkor a kérdezett magasság 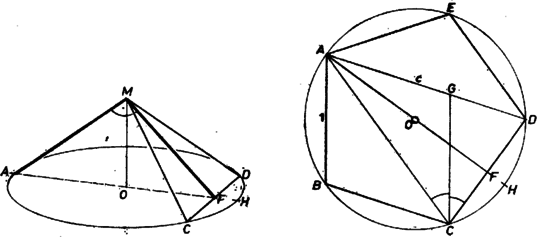$\sqrt[]{\bar{A O} \cdot \bar{O F}}$ .

Jelöljük az

A C D

háromszög

C

-beli szögfelezőjének a szemközti oldallal alkotott metszéspontját

G

-vel. Ekkor

\begin{matrix} C D G ∢ = D G C ∢ = 72^{\circ}, A C G ∢ = C A G ∢ = 36^{\circ}, \end{matrix}

tehát

A G = G C = C D = 1

, így az

A D

átló

c

hosszára az

A C D

és

C D G

háromszögek hasonlósága alapján az aranymetszést jelentő

\begin{matrix} c : 1 = 1 : (c - 1) \end{matrix}

másodfokú egyenletet írhatjuk fel, amiből

c > 1

miatt

c = (\sqrt[]{5} + 1) / 2

következik.
Jelöljük másrészt az

A B C D E

ötszög köré írható kör

A

-val átellenes pontját

H

-val, a kör sugarát

r

-rel,

A F

hosszát

f

-fel. Az átfogó darabjaira vonatkozó tételt használva kapjuk, hogy

A H \cdot A F = A D^{2}

, vagyis

r = c^{2} / 2 f

. Pitagorasz tétele alapján

f^{2} = c^{2} - 1 / 4

, tehát

\begin{matrix} A O \cdot O F = r (f - r) = \frac{c^{2}}{2} - \frac{c^{4}}{4 c^{2} - 1} = \frac{1}{2} \frac{c^{2} (2 c^{2} - 1)}{4 c^{2} - 1} = \\ = \frac{1}{2} \frac{(c + 1) (2 c + 1)}{4 c + 3} = \frac{1}{2} \frac{5 c + 3}{4 c + 3} = \frac{1}{2} + \frac{1}{4} \frac{\sqrt[]{5} + 1}{2 \sqrt[]{5} + 5} = \frac{3 \sqrt[]{5} + 5}{20} . \end{matrix}

(Közben többször felhasználtuk, hogy

c^{2} = c + 1.)

Tehát a kérdezett magasság

\frac{1}{2} \sqrt[]{\frac{3 \sqrt[]{5} + 5}{5}} = 0, 76512